题目内容
16.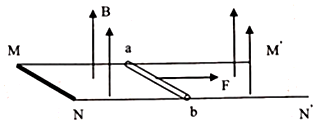 如图所示,质量为M的U型金属框M′MNN′,静放在粗糙绝缘水平面上(动摩擦因数为μ),且最大静摩擦力等于滑动摩擦力.MM′、NN′边相互平行,相距为L,电阻不计且足够长,底边MN垂直于MM′,电阻为r.质量为m的光滑导体棒ab电阻为R,垂直MM′放在框架上,整个装置处于垂直轨道平面向上.磁感应强度大小为B的匀强磁场中.在与ab垂直的水平拉力作用下,ab沿轨道由静止开始做匀加速直线运动,经x距离后撤去拉力,直至最后停下,整个过程中框架恰好没动.若导体棒ab与MM′、NN′始终保持良好接触,求:
如图所示,质量为M的U型金属框M′MNN′,静放在粗糙绝缘水平面上(动摩擦因数为μ),且最大静摩擦力等于滑动摩擦力.MM′、NN′边相互平行,相距为L,电阻不计且足够长,底边MN垂直于MM′,电阻为r.质量为m的光滑导体棒ab电阻为R,垂直MM′放在框架上,整个装置处于垂直轨道平面向上.磁感应强度大小为B的匀强磁场中.在与ab垂直的水平拉力作用下,ab沿轨道由静止开始做匀加速直线运动,经x距离后撤去拉力,直至最后停下,整个过程中框架恰好没动.若导体棒ab与MM′、NN′始终保持良好接触,求:(1)加速过程中通过导体棒ab的电量q;
(2)导体棒ab的最大速度vm以及匀加速阶段的加速度;
(3)导体棒ab走过的总位移.
分析 (1)根据法拉第电磁感应定律、闭合电路的欧姆定律结合电荷量的计算公式求解电荷量;
(2)对框架根据共点力的平衡条件求解导体棒的最大速度;根据匀变速直线运动位移速度关系求解加速度;
(3)撤去力后导体棒在安培力作用下做减速运动,由动量定理列方程求解减速位移,从而求解总路程.
解答 解:(1)根据法拉第电磁感应定律可得:E=$\frac{△Φ}{△t}$,
感应电流为:I=$\frac{E}{R+r}$,
根据电荷量的计算公式可得:
q=I△t=$\frac{△Φ}{R+r}$=$\frac{BLx}{R+r}$;
(2)由题意可知当框架恰好不动时,导体棒速度最大,对框架根据共点力的平衡条件可得:
FA=f=μ(M+m)g,
根据安培力的计算公式可得:
FA=BIL=$\frac{{B}^{2}{L}^{2}{v}_{m}}{R+r}$,
联立解得:vm=$\frac{μg(M+m)(r+R)}{{B}^{2}{L}^{2}}$;
根据匀变速直线运动位移速度关系可得:
${v}_{m}^{2}=2ax$,
解得:a=$\frac{{μ}^{2}{g}^{2}(M+m)^{2}(r+R)^{2}}{{2B}^{4}{L}^{4}}$;
(3)撤去力后导体棒在安培力作用下做减速运动,由动量定理可知:
$B\overline{I}Lt=m{v}_{m}-0$,
即:$\frac{{B}^{2}{L}^{2}\overline{v}t}{R+r}=m{v}_{m}$,
而以后运动的位移为:x′=$\overline{v}t$,
解得:x′=$\frac{μmg(M+m)(r+R)^{2}}{{B}^{4}{L}^{4}}$,
所以总路程为:s=x+x′=x+$\frac{μmg(M+m){(r+R)}^{2}}{{B}^{4}{L}^{4}}$.
答:(1)加速过程中通过导体棒ab的电量为$\frac{BLx}{R+r}$;
(2)导体棒ab的最大速度为$\frac{μg(M+m)(r+R)}{{B}^{2}{L}^{2}}$,匀加速阶段的加速度为$\frac{{μ}^{2}{g}^{2}{(M+m)}^{2}{(r+R)}^{2}}{{2B}^{4}{L}^{4}}$;
(3)导体棒ab走过的总位移为x+$\frac{μmg(M+m){(r+R)}^{2}}{{B}^{4}{L}^{4}}$.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解;如果涉及安培力作用下求位移问题,首先要考虑到动量定理.

 阅读快车系列答案
阅读快车系列答案 用能量为12.30eV的光子去照射一群处于基态的氢原子,则受到光的照射后下列关于氢原子跃迁的说法正确的是( )
用能量为12.30eV的光子去照射一群处于基态的氢原子,则受到光的照射后下列关于氢原子跃迁的说法正确的是( )| A. | 电子能跃迁到n=2的能级上去 | B. | 电子能跃迁到n=3的能级上去 | ||
| C. | 电子能跃迁到n=4的能级上去 | D. | 电子不能跃迁到其他能级上去 |
 如图所示,真空中有两个等量异种电荷,OO′为两电荷连线的垂直平分线.p点在垂直平分线上,四边形ONPM为菱形,现在将一个负电荷q,自O点开始沿ONPM移动,下列说法正确的是( )
如图所示,真空中有两个等量异种电荷,OO′为两电荷连线的垂直平分线.p点在垂直平分线上,四边形ONPM为菱形,现在将一个负电荷q,自O点开始沿ONPM移动,下列说法正确的是( )| A. | 由O到N的过程中电荷电势能增加 | B. | 由N到p的过程中电场力做负功 | ||
| C. | N点和M点场强相同 | D. | p点和O点电势相等 |

| A. | 线框中有从a→b的感应电流 | B. | 线框中有从b→a的感应电流 | ||
| C. | a、b两点间电势差等于0 | D. | a、b两点间电势差不等于0 |
 如图所示,光滑斜面倾角为θ,虚线M、N之间有沿斜面向上的匀强电场,完全相同的两块带电绝缘薄板A、B并排放在斜面上,A、B不粘连,A的下端到M的距离为L.每块板长为L,质量为m,带电量为+q,电荷在绝缘板上分布均匀,M、N之间距离为3L,电场强度E=$\frac{mgsinθ}{q}$,重力加速度为g,A、B两板间的库仑力不计,将A、B由静止释放,求:
如图所示,光滑斜面倾角为θ,虚线M、N之间有沿斜面向上的匀强电场,完全相同的两块带电绝缘薄板A、B并排放在斜面上,A、B不粘连,A的下端到M的距离为L.每块板长为L,质量为m,带电量为+q,电荷在绝缘板上分布均匀,M、N之间距离为3L,电场强度E=$\frac{mgsinθ}{q}$,重力加速度为g,A、B两板间的库仑力不计,将A、B由静止释放,求: 在“探究力的平行四边形定则”实验中,某同学用两个弹簧测力计将橡皮筋的端点拉到点O后,作出了这两个拉力F1、F2的图示,再改用一个弹簧测力计将橡皮筋的端点拉到同一点O,此时弹簧测力计的示数为F3=5.0N
在“探究力的平行四边形定则”实验中,某同学用两个弹簧测力计将橡皮筋的端点拉到点O后,作出了这两个拉力F1、F2的图示,再改用一个弹簧测力计将橡皮筋的端点拉到同一点O,此时弹簧测力计的示数为F3=5.0N
 如图,POQ是折成60°角的固定于竖直平面内的光滑金属导轨,导轨关于竖直轴线对称,OP=OQ=L=$\sqrt{3}$m,整个装置处在垂直导轨平面向里的足够大的匀强磁场中,磁感应强度随时间变化规律为B=1-8t(T).一质量为1kg、长为L、电阻为1Ω、粗细均匀的导体棒锁定于OP、OQ的中点a、b位置.当磁感应强度变为B1=0.5T 后保持不变,同时将导体棒解除锁定,导体棒向下运动,离开导轨时的速度为v=3.6m/s.导体棒与导轨始终保持良好接触,导轨电阻不计,重力加速度为g=10m/s2.求导体棒:
如图,POQ是折成60°角的固定于竖直平面内的光滑金属导轨,导轨关于竖直轴线对称,OP=OQ=L=$\sqrt{3}$m,整个装置处在垂直导轨平面向里的足够大的匀强磁场中,磁感应强度随时间变化规律为B=1-8t(T).一质量为1kg、长为L、电阻为1Ω、粗细均匀的导体棒锁定于OP、OQ的中点a、b位置.当磁感应强度变为B1=0.5T 后保持不变,同时将导体棒解除锁定,导体棒向下运动,离开导轨时的速度为v=3.6m/s.导体棒与导轨始终保持良好接触,导轨电阻不计,重力加速度为g=10m/s2.求导体棒: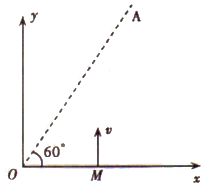 如图所示,在第一象限内有一正三角形区域的有界匀强磁场(未画出),方向垂直纸面向里,磁感应强度大小B=0.5T,一比荷为2×102C/kg的带正电粒子,从M点以v=200m/s的速度垂直x轴方向射入第一象限,粒子射出磁场时,速度方向恰好与OA直线垂直.不计粒子的重力,则:
如图所示,在第一象限内有一正三角形区域的有界匀强磁场(未画出),方向垂直纸面向里,磁感应强度大小B=0.5T,一比荷为2×102C/kg的带正电粒子,从M点以v=200m/s的速度垂直x轴方向射入第一象限,粒子射出磁场时,速度方向恰好与OA直线垂直.不计粒子的重力,则: