题目内容
如图所示，在半径为R的半圆形碗的光滑表面上，一质量为m的小球在水平面内作匀速圆周运动，周期为T，则该平面离碗底的距离h=R-
| gT2 |
| 4π2 |
R-
．| gT2 |
| 4π2 |
分析：小球在光滑碗内靠重力和支持力的合力提供向心力，根据向心力和重力的关系求出小球与半球形碗球心连线与竖直方向的夹角，根据几何关系求出平面离碗底的距离h．
解答：解：小球靠重力和支持力的合力提供向心力，如图所示：
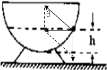
小球做圆周运动的半径为r=Rsinθ，根据力图可知tanθ=
=
；
解得cosθ=
．
所以h=R-Rcosθ=R-
=R-
．
故答案为：R-
．
小球做圆周运动的半径为r=Rsinθ，根据力图可知tanθ=
| F向 |
| mg |
| mRsinθω2 |
| mg |
解得cosθ=
| g |
| Rω2 |
所以h=R-Rcosθ=R-
| g |
| ω2 |
| gT2 |
| 4π2 |
故答案为：R-
| gT2 |
| 4π2 |
点评：解决本题的关键知道小球做圆周运动向心力的来源，运用牛顿第二定律和几何关系进行求解．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，在半径为R的圆形区域内，有匀强磁场，磁感应强度为B，方向垂直于圆平面（未画出）．一群比荷都为α的负离子体以相同速率v0（较大），由P点在纸平面内向不同方向射入磁场中发生偏转后，又飞出磁场，则下列说法正确的是（不计重力） （ ）
如图所示，在半径为R的圆内有一磁感应强度为B的向外的匀强磁场，一质量为m、电量为q的粒子（不计重力），从A点对着圆心方向垂直射入磁场，从C点飞出，则下列说法不正确的是（ ）
（2013?南宁三模）如图所示，在半径为R的圆形区域内有一匀强磁场，磁感应强度为B，方向垂直圆面向内．有一个质量为m，带电量为q的粒子，从A点沿半径方向垂直射人磁场内，又从C点射出，∠AOC=120°，下列说法正确的是（ ）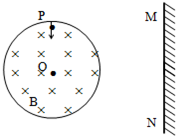
如图所示，在半径为R=
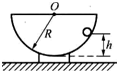如图所示，在半径为R的半圆形碗的光滑表面上，一质量为m的小球以角速度ω在水平面内作匀速圆周运动，此时球对碗的压力FN=