题目内容
3．某种气体的温度是0℃，可以说（ ）| A． | 气体中分子的温度是0℃ | |
| B． | 气体中分子运动的速度快的温度一定高于0℃，运动慢的温度一定低于0℃，所以气体平均温度是0℃ | |
| C． | 气体温度升高时，速率小的分子数目减少，速率大的分子数目增加 | |
| D． | 该气体没有内能 |
分析 从分子运动论观点看，温度是物体分子运动平均动能的标志．温度是大量分子热运动的集体表现，含有统计意义．对于个别分子来说，温度是没有意义的
解答 解：AB、温度是物体分子运动平均动能的标志．温度是大量分子热运动的集体表现，含有统计意义．对于个别分子来说，温度是没有意义的．故AB错误．
C、温度是物体分子运动平均动能的标志．从统计规律上看，气体温度升高时，速率小的分子数目减少，速率大的分子数目增加，故C正确
D、分子做无规则运动，故分子内能永不为零，故D错误
故选：C
点评 温度是物体内分子热运动的宏观表现，温度是表示物体冷热程度的物理量，微观上来讲是物体分子热运动的剧烈程度．温度是物体内分子间平均动能的一种表现形式．分子运动愈快，物体愈热，即温度愈高；分子运动愈慢，物体愈冷，即温度愈低
练习册系列答案
相关题目
13．
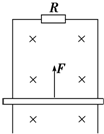如图所示，竖直放置的两根平行金属导轨间距为l，之间接有定值电阻R，质量为m的金属棒与两导轨始终保持垂直并良好接触且无摩擦，棒的电阻为r，导轨电阻不计．整个装置放在磁感应强度为B的匀强磁场中，磁场方向与导轨平面垂直，棒在竖直向上的恒力F作用下先加速上升的一段时间，再达到稳定状态．则下列说法中正确的是（ ）
如图所示，竖直放置的两根平行金属导轨间距为l，之间接有定值电阻R，质量为m的金属棒与两导轨始终保持垂直并良好接触且无摩擦，棒的电阻为r，导轨电阻不计．整个装置放在磁感应强度为B的匀强磁场中，磁场方向与导轨平面垂直，棒在竖直向上的恒力F作用下先加速上升的一段时间，再达到稳定状态．则下列说法中正确的是（ ）| A． | 棒达到稳定状态时，通过它的电流为I=$\frac{（F-mg）}{Bl}$ | |
| B． | 棒达到稳定状态时，其速度为v=$\frac{（F-mg）R}{{B}^{2}{l}^{2}}$ | |
| C． | 棒达到稳定状态前，其加速度一直在减小 | |
| D． | 整个过程中，棒所受安培力做功在数值上等于棒上所生的热 |
14．有一简谐波沿x轴正向传播，当波上某质点A向上运动到最大位移时，在其右方相距1.5m的质点B刚好在平衡位置向上运动，则该波的波长可能是（ ）
| A． | 1.0m | B． | 1.2m | C． | 1.6m | D． | 2.0m |
如图所示，一个质量为m的小球用一根长为L的细绳吊在天花板上，给小球一水平初速度，使它做匀速圆周运动，小球运动所在的平面是水平的．已知细绳与竖直方向的夹角为θ，重力加速度为g．求：
18．
某学习小组的同学在用多用电表研究热敏特性实验中，安装好如图所示的装置．向杯内加入冷水，温度计的示数为20℃，多用电表选择适当的倍率，读出热敏电阻的阻值R1．然后向杯内加入热水，温度计的示数为60℃，发现多用电表的指针偏转角度较大，则下列说法正确的是（ ）
某学习小组的同学在用多用电表研究热敏特性实验中，安装好如图所示的装置．向杯内加入冷水，温度计的示数为20℃，多用电表选择适当的倍率，读出热敏电阻的阻值R1．然后向杯内加入热水，温度计的示数为60℃，发现多用电表的指针偏转角度较大，则下列说法正确的是（ ）| A． | 多用电表应选用电流挡，温度升高换用大量程测量 | |
| B． | 多用电表应选用电流挡，温度升高换用小量程测量 | |
| C． | 多用电表应选用欧姆挡，温度升高时换用倍率大的档 | |
| D． | 多用电表应选用欧姆挡，温度升高时换用倍率小的档 |
8．下列哪些情况中力做的功为零（ ）
| A． | 竖直向上抛出一物体，上升过程中重力对物体做的功 | |
| B． | 卫星做匀速圆周运动时，卫星受到的引力对卫星所做的功 | |
| C． | 汽车匀速上坡时，车厢底部支撑力对货物所做的功 | |
| D． | 汽车匀速上坡时，车厢底部摩擦力对货物所做的功 |
12．如图甲、乙是配电房中的互感器和电表的接线图，下列说法中正确的是（ ）
| A． | 线圈匝数n1＜n2，n3＜n4 | |
| B． | 线圈匝数n1＞n2，n3＞n4 | |
| C． | 甲图中的电表是电流表，输出端不可短路 | |
| D． | 乙图中的电表是电流表，输出端不可断路 |
3．
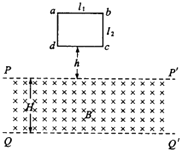如图所示，矩形平面导线框abcd位于竖直平面内，水平边ab长l1，竖直边bc长l2，线框质量为m，电阻为R．线框下方有一磁感应强度为B、方向与线框平面垂直的匀强磁场区域，该区域的上、下边界PP′和QQ′均与ab平行，两边界间的距离为H，H＞l2．让线框从dc边距边界PP′的距离为h处自由下落，已知在dc边进人磁场后、ab边到达边界PP′前的某一时刻，线框的速度已达到这一阶段的最大值，重力加速度为g，则（ ）
如图所示，矩形平面导线框abcd位于竖直平面内，水平边ab长l1，竖直边bc长l2，线框质量为m，电阻为R．线框下方有一磁感应强度为B、方向与线框平面垂直的匀强磁场区域，该区域的上、下边界PP′和QQ′均与ab平行，两边界间的距离为H，H＞l2．让线框从dc边距边界PP′的距离为h处自由下落，已知在dc边进人磁场后、ab边到达边界PP′前的某一时刻，线框的速度已达到这一阶段的最大值，重力加速度为g，则（ ）| A． | 当dc边刚进磁场时，线框速度为$\sqrt{2gh}$ | |
| B． | 当ab边刚到达边界PP′时，线框速度为$\frac{mgR}{{B}^{2}{{l}_{2}}^{2}}$ | |
| C． | 当dc边刚到达边界QQ′时，线框速度为$\sqrt{（\frac{mgR}{{B}^{2}{{l}_{1}}^{2}}）^{2}+2g（H-{l}_{2}）}$ | |
| D． | 从线框开始下落到dc边刚到达边界的QQ′过程中，线框产生的焦耳热为mg（h+l2）-$\frac{{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{{l}_{2}}^{4}}$ |