题目内容
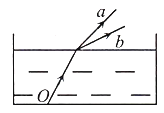
【题目】如图所示为某种透明材料制成的一块棱镜，其截面由直角三角形ABC和四分之一圆拼接而成。C点是圆弧BED的圆心，圆弧半径为R，BC⊥AC，且
，O点为AB边的中点。一束光线从O点入射，入射角为
，经棱镜折射后，恰好过C点。已知光在空气中的速度为c，求：（结果可保留根式。下列数据可供参考：
，
，
）
(1)透明材料的折射率；
(2)光线在棱镜中经历的时间；
(3)让入射光线缓慢绕O点逆时针旋转，当入射角减小到某一角度时，将有光线从AC边上的F点射出（图中没标出），求F点到C点的距离。
【答案】(1)
；(2)
；(3)
【解析】
(1)折射光恰好经过C点，则折射角为
，因此折射率为
(2)设光在棱镜中发生全发射的临界角为
，由
可得
光线在棱镜中发生全反射，其路程为
，则光在棱镜中的速度为
则光在棱镜中经历的时间为
(3)作图可得
全反射的临界角为
在
中
则
由正弦定理可得
其中
由此可得
练习册系列答案
相关题目
