题目内容
 如图所示,一长为
如图所示,一长为| 2 |
分析:欲使小球恰好落到木板下端,根据平抛运动在水平方向和竖直方向上的运动规律,抓住位移关系求出平抛运动的时间,根据碰撞前后的速度大小相等,求出自由落体和平抛运动的时间关系,从而求出下降的高度关系,根据几何关系求出球释放点距木板上端的水平距离.
解答:解:根据平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,有:tan45°=
,解得t=
.
物体自由下落的时间为t′=
.
根据h=
gt2知,平抛运动在竖直方向上的位移和自由落体运动的位移之比为4:1,木板在竖直方向上的高度为L,则碰撞点竖直方向上的位移为
.所以小球释放点距木板上端的水平距离为
.
故答案为:
.
| ||
| vt |
| 2v |
| g |
物体自由下落的时间为t′=
| v |
| g |
根据h=
| 1 |
| 2 |
| L |
| 5 |
| L |
| 5 |
故答案为:
| L |
| 5 |
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,灵活运用运动学公式进行求解.

练习册系列答案
相关题目
 如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端分别固定小球A和B,小球A和B质量分别为m和2m,光滑的铁钉穿过轻杆小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力,下列说法正确的是( )
如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端分别固定小球A和B,小球A和B质量分别为m和2m,光滑的铁钉穿过轻杆小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力,下列说法正确的是( ) (2010?长春一模)如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( )
(2010?长春一模)如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( )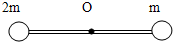 如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( )
如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( )