题目内容
 如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端分别固定小球A和B,小球A和B质量分别为m和2m,光滑的铁钉穿过轻杆小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力,下列说法正确的是( )
如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端分别固定小球A和B,小球A和B质量分别为m和2m,光滑的铁钉穿过轻杆小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力,下列说法正确的是( )分析:两球组成的系统在转动过程中,只有重力做功,其机械能守恒,即可知两球机械能变化的关系,及总重力势能的减少与总动能增加的关系.转动到竖直位置时,两球的速度大小相等,运用机械能守恒定律求出此两球的速度大小.由机械能守恒分析,两球是否能做完整的圆周运动.
解答:解:
A、对于两球组成的系统,在转动过程中,只有重力做功,其机械能守恒.而转动过程中,A的机械能增加,B的机械能减少,则由机械能守恒定律得知,A球机械能的增加等于B球机械能的减少.故A错误.
B、对于两球组成的系统,在转动过程中,总重力势能减少,总动能增加,由机械能守恒定律得知,两球的总重力势能的减少等于总动能的增加.故B正确.
C、设转到竖直位置时两球的速度大小为v,则由机械能守恒定律有
2mgL-mgL=
mv2+
?2mv2,解得,v=
.故C错误.
D、由机械能守恒定律分析得知,当系统顺时针转到水平位置时速度为零,然后再逆时针转动,不可能做完整的圆周运动.故D错误.
故选B
A、对于两球组成的系统,在转动过程中,只有重力做功,其机械能守恒.而转动过程中,A的机械能增加,B的机械能减少,则由机械能守恒定律得知,A球机械能的增加等于B球机械能的减少.故A错误.
B、对于两球组成的系统,在转动过程中,总重力势能减少,总动能增加,由机械能守恒定律得知,两球的总重力势能的减少等于总动能的增加.故B正确.
C、设转到竖直位置时两球的速度大小为v,则由机械能守恒定律有
2mgL-mgL=
| 1 |
| 2 |
| 1 |
| 2 |
|
D、由机械能守恒定律分析得知,当系统顺时针转到水平位置时速度为零,然后再逆时针转动,不可能做完整的圆周运动.故D错误.
故选B
点评:本题是轻杆连接的连接体问题,属于系统机械能守恒的类型,由机械能守恒定律分析两个物体机械能变化关系和动能与势能变化关系.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 (2010?长春一模)如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( )
(2010?长春一模)如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( )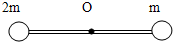 如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( )
如图所示,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( ) 如图所示,一长为
如图所示,一长为