题目内容
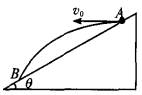
如图所示,在倾角为θ的斜面上一点A以初速度ν0水平抛出一小球,最后落在斜面上B点,不计空气阻力.求:
(1)小球在空中运动时间t及到B点的速度大小ν1.
(2)小球何时离斜面最远?此时小球的速度是多大?
答案:
解析:
提示:
解析:
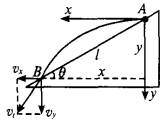
解析:小球做的是平抛运动,如图所示.AB长度为其实际位移,设为l.
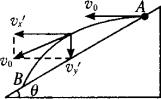
(1)由平抛运动的规律,水平方向上有lcos (2)经分析可知,当小球的速度平行于斜面时,小球离斜面的距离最远,设此点为C点,如图所示.由速度三角形关系可得νy′=νx′tan
|
提示:
点拨:本题考查的是平抛运动的基本规律.第一问是个常规问题;第二问的求解,判断出小球在什么位置时离斜面最远是解题的关键.本题还有较巧妙的解法.第一问中,当小球落到斜面上时,其位移与水平方向的夹角为θ,利用左边的结论可知,其速度与水平方向夹角的正切值必为2tan |

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图所示,在倾角为θ=37°的斜面两端,垂直于斜面方向固定两个弹性板,两板相距d=2m,质量为m=10g,带电量为q=+1×10-7C的物体与斜面间的动摩擦因数为μ=0.2,物体从斜面中点以大小为v0=10m/s的速度沿斜面开始运动.若物体与弹性板碰撞过程中机械能不损失,电量也不变,匀强电场(方向与斜面平行)的场强E=2×106N/C,求物体在斜面上运动的总路程.(g取10m/s2 sin37°=0.6 cos37°=0.8)
如图所示,在倾角为θ=37°的斜面两端,垂直于斜面方向固定两个弹性板,两板相距d=2m,质量为m=10g,带电量为q=+1×10-7C的物体与斜面间的动摩擦因数为μ=0.2,物体从斜面中点以大小为v0=10m/s的速度沿斜面开始运动.若物体与弹性板碰撞过程中机械能不损失,电量也不变,匀强电场(方向与斜面平行)的场强E=2×106N/C,求物体在斜面上运动的总路程.(g取10m/s2 sin37°=0.6 cos37°=0.8) (2009?上海模拟)如图所示,在倾角为30°、静止的光滑斜面上,一辆加速下滑的小车上悬吊单摆的摆线总处于水平位置.已知车的质量和摆球的质量均为m,下列正确的是( )
(2009?上海模拟)如图所示,在倾角为30°、静止的光滑斜面上,一辆加速下滑的小车上悬吊单摆的摆线总处于水平位置.已知车的质量和摆球的质量均为m,下列正确的是( ) 如图所示,在倾角为θ的绝缘斜面上,有相距为L的A、B两点,分别固定着两个带电量均为Q的正点电荷.O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=
如图所示,在倾角为θ的绝缘斜面上,有相距为L的A、B两点,分别固定着两个带电量均为Q的正点电荷.O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=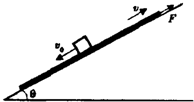 如图所示,在倾角为θ=37°的足够长的斜面上,有质量为m1=2kg的长木板.开始时,长木板上有一质量为m2=1kg的小铁块(视为质点)以相对地面的初速度v0=2m/s 从长木板的中点沿长木板向下滑动,同时长木板在沿斜面向上的拉力作用下始终做速度为v=1m/s的匀速运动,小铁块最终与长木板一起沿斜面向上做匀速运动.已知小铁块与长木板、长木板与斜面间的动摩擦因数均为μ=0.9,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8
如图所示,在倾角为θ=37°的足够长的斜面上,有质量为m1=2kg的长木板.开始时,长木板上有一质量为m2=1kg的小铁块(视为质点)以相对地面的初速度v0=2m/s 从长木板的中点沿长木板向下滑动,同时长木板在沿斜面向上的拉力作用下始终做速度为v=1m/s的匀速运动,小铁块最终与长木板一起沿斜面向上做匀速运动.已知小铁块与长木板、长木板与斜面间的动摩擦因数均为μ=0.9,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8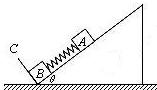 如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态,现开始用一恒力F沿斜面方向拉物块A使之向上运动,重力加速度为g,问:
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态,现开始用一恒力F沿斜面方向拉物块A使之向上运动,重力加速度为g,问: