题目内容
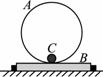
如图所示，竖直圆环A半径为r，固定在木板B上，木板B放在水平地面上，B的左右两侧各有一挡板固定在地面上，使B不能左右移动，在环的最低点静止放置一个小球C。A、B、C的质量均为m，给小球一水平向右的瞬时速度，小球会在环内侧做圆周运动。不计一切摩擦，重力加速度为g，为保证小球能通过环的最高点，且不会使环在竖直方向上跳起，瞬时速度必须满足
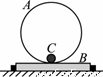
A．最小值为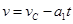
B．最小值为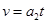
C．最大值为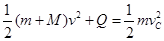
D．最大值为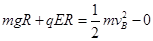
【答案】
BD
【解析】
试题分析：小球通过最高点时，重力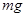
和轨道向下的弹力
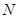的合力提供向心力，即
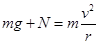，对AB整体分析，此时受到小球竖直向上的弹力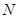，要是AB不跳起来，就要满足
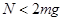，即
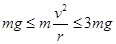，那么就有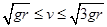
，从最低点到最高点，根据动能定理有
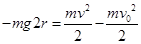，整理得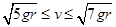
，对照答案BD对AC错。
考点：圆周运动 动能定理
练习册系列答案
相关题目
如图所示，竖直圆环内侧凹槽光滑，aOd为其水平直径，两个相同的均可视为质点的小球A和B，从a点以相同速率v0同时分别向上、向下沿圆环凹槽运动，且运动中始终未脱离圆环，则A、B两球第一次相遇（ ）
如图所示，竖直圆环中有多条起始于A点的光滑轨道，其中AB通过环心O并保持竖直．一质点分别自A点沿各条轨道下滑，初速度均为零．那么，质点沿各轨道下滑的时间相比较（ ）
（2005?青浦区模拟）如图所示，竖直圆环内侧凹槽光滑，aob为其水平直径，2个相同的小球A和B（均可视为质点），从a点同时以相同速率V0开始向上、向下沿圆环凹槽运动，且运动中始终未脱离圆环，则（ ）
B．最小值为
D．最大值为
