Question

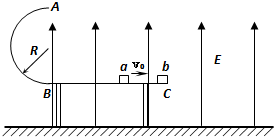如图所示，长l=2m水平绝缘台面处于竖直向上的匀强电场中，a、b是两个形状相同的金属小滑块，b滑块的质量是a滑块质量的5倍，b滑块不带电，放在水平台面的右边缘C处，台面左端B平滑地连接半径为R=0.32m的光滑半圆环AB，光滑半圆环处在匀强电场之外．已知a滑块带正电荷，与台面间的动摩擦因数μ=0.45．开始时给a滑块一个水平向右的初速度，大小为v₀=10m/s，滑块恰好能在台面上做匀速运动，之后与b滑块发生正碰，碰后b滑块落到地面上．设碰撞时间极短，碰后总电荷量没有损失且平分，a滑块还在桌面上，且平台右端的电场足够宽，不计a、b间的库仑力．已知台面高度h=0.5m，g取l0m/s²，碰撞后a滑块恰好能通过圆环的最高点，求滑块b落地时的速度．

Answer 1

分析：滑块a在A点时，重力提供向心力；B到A的过程中重力做功，在水平面时一定时摩擦力做功，根据动能定理即可求得a碰撞后的速度；
碰撞的过程中满足动量守恒定律，求得b的速度；碰撞后b做类平抛运动，根据平抛运动的规律即可求解．

解答：解：滑块a过A点时mg=m

v 2 A

R

滑块a由B沿圆环运动到A：

1

2

m

v

2 A

=mg?2R+

1

2

m

v

2 B

；

v

B

=

5gR

=4m/s；
滑块a由C滑到B：-μ

1

2

mgl=

1

2

m

v

2 B

-

1

2

m

v

2 a

代入数据，求得v_a=5m/s；
规定向右为正，则滑块a、b碰撞时：mv₀=-mv_a+5mv_b
代入数据，求得v_b=3m/s；
碰撞后，滑块b做类平抛运动，等效重力加速度a=

5mg- 1 2 mg

5m

=0.9g
落地时竖直方向的速度vy=

2ah

=

2×0.9×10×0.5

=3m/s
故落地时速度的大小为v=

v 2 y + v 2 b

=3

2

m/s；
速度的方向与水平方向成45°的角．  
答：滑块b落地时的速度大小为3

2

m/s，速度的方向与水平方向成45°的角．

点评：该题中涉及的运动过程比较多，而且用到的物理规律也比较多，一定要理清物体的运动过程，找到第一的规律．然后进行解答．