题目内容
制作半导体时,需向单晶硅或其他晶体中掺入杂质.单晶硅内的原子是规则排列的,在两层电子间的间隙会形成如图甲所示的上下对称的匀强电场,设某空间存在上下对称的匀强电场,并在该电场中的下半区域加一方向垂直纸面向里的匀强磁场,如图乙所示.电量为+q、质量为m的带电小球从上边界以初速度v垂直电场入射.已知上下场区的宽均为d,长为L,电场强度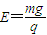 ,初速度
,初速度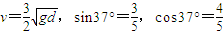 .
.求:
(1)小球第一次经过对称轴OO′时的速度;
(2)要使小球不越过下边界,所加磁场的磁感应强度B的最小值;
(3)若所加磁场的磁感应强度
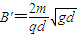 ,且L=20d,求小球在场区运动的总时间.
,且L=20d,求小球在场区运动的总时间.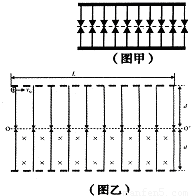
【答案】分析:(1)对小球受力分析,得知重力和电场力方向相同,由此可知小球在上半区的加速度,小球在上半区做类平抛运动,由牛顿运动定律和运动学公式几何速度的合成与分解可求出小球刚要离开上半区是的速度大小和方向.
(2)小球进入下边界,受到的电场力和重力平衡,小球在洛伦兹力的作用下做匀速圆周运动,画出运动轨迹图,由几何关系求出运动半径,在由牛顿运动定律可求出磁场的强度.
(3)首先可根据第二问的结果判知在此磁场中运动的半径(为第二问求得半径的一半),分析得出小球在做周期性的运动(在上半区做斜上抛运动,在下半区做匀速圆周运动),由几何知识求出一个周期内小球在水平方向上的位移,判断能运动几个周期;再分段求出一个周期所用的时间,便可求出总时间.
解答:解:
(1)小球进入电场后做类平抛运动,在竖直方向上有:
加速度:
竖直方向的位移:
得: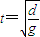
所以和速度大小为: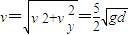
与竖直方向的夹角θ: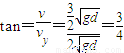
可得:θ=37°
(2)小球进入下半区域时,因重力和电场力平衡,小球在洛伦兹力的作用下做匀速匀速圆周运动,设小球恰好不越过下边界,则小球在到下边界时速度的方向应与边界平行,设圆周半径为R.如图所示: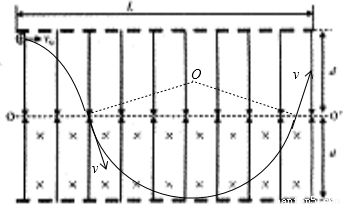
由几何关系得: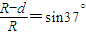
得:
由牛顿第二定律得: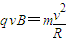
解得:
所以电磁场感应强度B的最小值为
(3)设在下半区域做圆周运动的轨道半径为R′,则结合第二问的知识有:

小球在场区做周期性运动,在一个周期内:
水平方向的位移:

周期:
因为L=20d,所以有:

答:(1)小球第一次经过对称轴OO′时的速度为
(2)要使小球不越过下边界,所加磁场的磁感应强度B的最小值为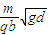
(3)小球在场区运动的总时间为
点评:正确分析带电粒子的受力及运动特征是解决问题的前提,灵活选用力学规律是解决问题的关键.
1、明确研究对象,对研究对象进行受力分析.
2、依据力与运动的关系,明确运动性质及运动过程作出运动轨迹?建立合理的运动模型.
3、根据不同的运动模型,选择合适的定律、定理列方程组求解.
当带电粒子在复合场中做匀速直线运动时,应根据平衡条件列方程求解.
当带电粒子在复合场中做匀速圆周运动时,应运用向心力公式和平衡条件联立方程求解.
当带电粒子在复合场中做非匀变速曲线运动时,应选用动能定理或能量守恒定律列方程求解.(或把该运动分解为匀速圆周运动和匀速直线运动的叠加)
(2)小球进入下边界,受到的电场力和重力平衡,小球在洛伦兹力的作用下做匀速圆周运动,画出运动轨迹图,由几何关系求出运动半径,在由牛顿运动定律可求出磁场的强度.
(3)首先可根据第二问的结果判知在此磁场中运动的半径(为第二问求得半径的一半),分析得出小球在做周期性的运动(在上半区做斜上抛运动,在下半区做匀速圆周运动),由几何知识求出一个周期内小球在水平方向上的位移,判断能运动几个周期;再分段求出一个周期所用的时间,便可求出总时间.
解答:解:
(1)小球进入电场后做类平抛运动,在竖直方向上有:
加速度:

竖直方向的位移:

得:
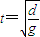
所以和速度大小为:
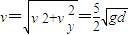
与竖直方向的夹角θ:
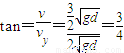
可得:θ=37°
(2)小球进入下半区域时,因重力和电场力平衡,小球在洛伦兹力的作用下做匀速匀速圆周运动,设小球恰好不越过下边界,则小球在到下边界时速度的方向应与边界平行,设圆周半径为R.如图所示:

由几何关系得:
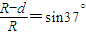
得:

由牛顿第二定律得:
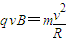
解得:

所以电磁场感应强度B的最小值为

(3)设在下半区域做圆周运动的轨道半径为R′,则结合第二问的知识有:

小球在场区做周期性运动,在一个周期内:
水平方向的位移:

周期:

因为L=20d,所以有:

答:(1)小球第一次经过对称轴OO′时的速度为

(2)要使小球不越过下边界,所加磁场的磁感应强度B的最小值为
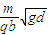
(3)小球在场区运动的总时间为

点评:正确分析带电粒子的受力及运动特征是解决问题的前提,灵活选用力学规律是解决问题的关键.
1、明确研究对象,对研究对象进行受力分析.
2、依据力与运动的关系,明确运动性质及运动过程作出运动轨迹?建立合理的运动模型.
3、根据不同的运动模型,选择合适的定律、定理列方程组求解.
当带电粒子在复合场中做匀速直线运动时,应根据平衡条件列方程求解.
当带电粒子在复合场中做匀速圆周运动时,应运用向心力公式和平衡条件联立方程求解.
当带电粒子在复合场中做非匀变速曲线运动时,应选用动能定理或能量守恒定律列方程求解.(或把该运动分解为匀速圆周运动和匀速直线运动的叠加)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?龙岩模拟)制作半导体时,需向单晶硅或其他晶体中掺入杂质.单晶硅内的原子是规则排列的,在两层电子间的间隙会形成如图甲所示的上下对称的匀强电场,设某空间存在上下对称的匀强电场,并在该电场中的下半区域加一方向垂直纸面向里的匀强磁场,如图乙所示.电量为+q、质量为m的带电小球从上边界以初速度v0垂直电场入射.已知上下场区的宽均为d,长为L,电场强度
(2011?龙岩模拟)制作半导体时,需向单晶硅或其他晶体中掺入杂质.单晶硅内的原子是规则排列的,在两层电子间的间隙会形成如图甲所示的上下对称的匀强电场,设某空间存在上下对称的匀强电场,并在该电场中的下半区域加一方向垂直纸面向里的匀强磁场,如图乙所示.电量为+q、质量为m的带电小球从上边界以初速度v0垂直电场入射.已知上下场区的宽均为d,长为L,电场强度 通过“30m折返跑”的测试成绩可以反应一个人的身体素质.在平直的跑道上,一学生站立在起点线A处,当听到起跑口令后(测试员同时开始计时),跑向正前方30m处的折返线,到达折返线B处时,用手触摸固定在折返线处的标杆,再转身跑回起点线,返程无需减速,到达起点线处时,停止计时,全过程所用时间即为折返跑的成绩.学生加速或减速过程均视为匀变速,触摸杆的时间不计.某同学加速时的加速度大小为a1=2.5m/s2,减速时的加速度大小为a2=5m/s2,到达折返线处时速度需减小到零,并且该生全过程中最大速度不超过vm=7.5m/s.求:
通过“30m折返跑”的测试成绩可以反应一个人的身体素质.在平直的跑道上,一学生站立在起点线A处,当听到起跑口令后(测试员同时开始计时),跑向正前方30m处的折返线,到达折返线B处时,用手触摸固定在折返线处的标杆,再转身跑回起点线,返程无需减速,到达起点线处时,停止计时,全过程所用时间即为折返跑的成绩.学生加速或减速过程均视为匀变速,触摸杆的时间不计.某同学加速时的加速度大小为a1=2.5m/s2,减速时的加速度大小为a2=5m/s2,到达折返线处时速度需减小到零,并且该生全过程中最大速度不超过vm=7.5m/s.求: