��Ŀ����
4�� �ڵ糡ǿ��ΪE����ǿ�糡�У�һ����糡��ƽ�е�ֱ������������ֹ��С��A��B�����ɿ����ʵ㣩����С���������Ϊm��A��������Ϊ+Q��B���磮��ʼʱ�������L��ֻ�ڵ糡���������£�A��ʼ��ֱ���˶�������B����������ײ����ײ��A��B������ܶ�������ʧ��A��B��������ת�ƣ��������ƣ��ʣ�
�ڵ糡ǿ��ΪE����ǿ�糡�У�һ����糡��ƽ�е�ֱ������������ֹ��С��A��B�����ɿ����ʵ㣩����С���������Ϊm��A��������Ϊ+Q��B���磮��ʼʱ�������L��ֻ�ڵ糡���������£�A��ʼ��ֱ���˶�������B����������ײ����ײ��A��B������ܶ�������ʧ��A��B��������ת�ƣ��������ƣ��ʣ���1��A���ʱ����B������һ����ײ��
��2����һ����ײ��A��B������ٶȸ�Ϊ���
��3����һ����ײ��Ҫ�����ʱ���ٴη�����ײ��
���� ��1������ţ�ٵڶ��������A��ļ��ٶȣ����ٶ�λ�ƹ�ʽ���A����B����ײǰ��ʱ�䣮
��2��������ײ������A��B�����ܶ�������ʧ�������ٶȣ����������غ�Ͷ����غ㶨����ʽ����ٶȣ�
��3����һ������A����B��λ�����ʱ�������ڶ���ײ����λ���������ڶ�����ײʱ�䣮
��� �⣺��1����С��A�ļ��ٶ�Ϊa������ʱ��t1��B������һ����ײ����
����ţ�ٵڶ�����֪��QE=ma
��λ��ʱ���ϵ֪L=$\frac{1}{2}a{t}_{1}^{2}$
���t1=$\sqrt{\frac{2mL}{QE}}$
��2����A��ײǰ���ٶ�Ϊv0����ײ��A��B���ٶȷֱ�Ϊv1��v2����
$\frac{1}{2}m{v}_{0}^{2}$=QEL
���ݶ����غ㶨��֪mv0=mv1+mv2
���������غ㶨��֪$\frac{1}{2}m{v}_{0}^{2}$=$\frac{1}{2}m{v}_{1}^{2}$$+\frac{1}{2}m{v}_{2}^{2}$
���v1=0��v2=$\sqrt{\frac{2QEL}{m}}$
��3�����һ����ײ����ʱ��t2��A��B�ٷ�����ײ����
$\frac{1}{2}a{t}_{2}^{2}$=v2t2
���t2=2$\sqrt{\frac{2mL}{QE}}$
�𣺣�1��A��t$\sqrt{\frac{2mL}{QE}}$��B������һ����ײ��
��2����һ����ײ��A��B������ٶȷֱ���v1=0��v2=$\sqrt{\frac{2QEL}{m}}$��
��3����һ����ײ��Ҫ����2$\sqrt{\frac{2mL}{QE}}$�ٴη�����ײ��
���� ������С���������˶����⣬�ۺ�Ӧ��ţ���˶����ɺ������غ㶨�ɡ������غ㶨�ɽ��⣬�������⣮

 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д� ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д� ��ͼ��ʾ�����徲ֹ�ڹ̶�б���ϣ�����ƽ��б�����ϵ���F�����壬����F����������Ĺ����У�����ʼ�ձ��־�ֹ����������Ħ�����ı仯����ǣ�������
��ͼ��ʾ�����徲ֹ�ڹ̶�б���ϣ�����ƽ��б�����ϵ���F�����壬����F����������Ĺ����У�����ʼ�ձ��־�ֹ����������Ħ�����ı仯����ǣ�������| A�� | һֱ���� | B�� | һֱ��С | C�� | �ȼ�С������ | D�� | ��ȷ�� |
| A�� | 0.5Сʱ | B�� | 1.4Сʱ | C�� | 4.2Сʱ | D�� | 12.6Сʱ |
| A�� | x=8��y=3 | B�� | x=9��y=5 | C�� | x=8��y=5 | D�� | x=9��y=4 |
| A�� | �������߾���ϡ�����嵼��ĻԹ�ŵ����� | |
| B�� | ��������������չ��������������ĵ����� | |
| C�� | ������������������ԭ�� | |
| D�� | �������߰�ֱ�ߴ��������ɱ��糡���ų�ƫת |
 ˮƽ�����Ͼ�ֹͣ��һƽ���꣬�����˵�������M=150kg������ m=50kg�����ᄇֹ�ھ�ƽ�峵���L=4m������ͼ��ʾ��������ˮƽ����ĺ㶨ˮƽ��F=300N ������ʱ������Գ�ʼ�ղ�����������ƽ�峵֮�䡢ƽ�峵�����֮����Ħ�������������뿪ƽ�峵�Ĺ����У�
ˮƽ�����Ͼ�ֹͣ��һƽ���꣬�����˵�������M=150kg������ m=50kg�����ᄇֹ�ھ�ƽ�峵���L=4m������ͼ��ʾ��������ˮƽ����ĺ㶨ˮƽ��F=300N ������ʱ������Գ�ʼ�ղ�����������ƽ�峵֮�䡢ƽ�峵�����֮����Ħ�������������뿪ƽ�峵�Ĺ����У�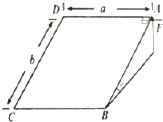 ��ͼ��ʾ���ֲ�б����Ǧ�=37�㣬б���aΪ3m����bΪ4m������Ϊ0.1kg��Сľ���б��A�㾲ֹ�ͷţ��ͷ�ͬʱ����б��ױ�BCƽ�еĺ���F�Ƹ�Сľ�飬Сľ����б���Ķ�Ħ������Ϊ��=0.5��gȡ10m/s2��sin37��=0.6��cos37��=0.8����
��ͼ��ʾ���ֲ�б����Ǧ�=37�㣬б���aΪ3m����bΪ4m������Ϊ0.1kg��Сľ���б��A�㾲ֹ�ͷţ��ͷ�ͬʱ����б��ױ�BCƽ�еĺ���F�Ƹ�Сľ�飬Сľ����б���Ķ�Ħ������Ϊ��=0.5��gȡ10m/s2��sin37��=0.6��cos37��=0.8����