题目内容
17. 如图所示,一个半径为R的非均质圆球,其重心不在球心O点,先将它置于水平地面上,平衡时球面上的A点和地面接触;再将它置于倾角为30°的粗糙斜面上,平衡时球面上的B点与斜面接触,已知A到B的圆心角也为30°,试求球体的重心C到球心O的距离.
如图所示,一个半径为R的非均质圆球,其重心不在球心O点,先将它置于水平地面上,平衡时球面上的A点和地面接触;再将它置于倾角为30°的粗糙斜面上,平衡时球面上的B点与斜面接触,已知A到B的圆心角也为30°,试求球体的重心C到球心O的距离.
分析 先将它置于水平地面上,平衡时球面上的A点和地面接触,支持力作用点在A点,重力的作用线必经过A,和OA在一条线上;当球在粗糙斜面上,受到三个力处于平衡,这三个力是共点力,已知支持力,摩擦力的作用点在B点,那么重力力作用线必经过B点与线OA交与点C,重心只有一个即C点,由几何关系可得.
解答 解:由上面的分析可知:C点为重心,由几何关系可得:
∠OBC=30o △OBC为等腰三角形
则2OCcos30°=R
解得:OC=$\frac{\sqrt{3}}{3}R$
点评 考查共点力的概念,共点力:作用于一点的力或者力的作用线交于一点的力.三力交汇原理:物体在三个力作用下平衡,则三个力不平行必然交于一点.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
7.国家836计划中的一个重点项目中所研究的X光激光(频率范围很窄的高强度X射线)有着广泛的应用前景,用X光激光给细胞“照相”,以下激光的哪些特点属于次要因素( )
| A. | 杀菌作用 | B. | 化学作用 | C. | 波长短 | D. | 能量高 |
8.下列说法正确的是( )
| A. | 任何物体之间都会产生弹力的作用 | |
| B. | 放在桌面上的物体受到了桌面对它的弹力是因为物体发生了弹性形变产生 | |
| C. | 绳对物体的拉力的方向总是沿着绳指向绳收缩的方向 | |
| D. | 形变物体产生的弹力的方向,总与其形变方向相反 |
5.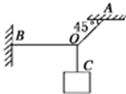 如图所示,能承受最大拉力为100N的细线OA与竖直方向成45°角,能承受最大拉力为5 0N的细线OB水平,细线OC能承受足够大的拉力,为使OA,OB均不被拉断,OC下端所悬挂物体的最大重力是多少?
如图所示,能承受最大拉力为100N的细线OA与竖直方向成45°角,能承受最大拉力为5 0N的细线OB水平,细线OC能承受足够大的拉力,为使OA,OB均不被拉断,OC下端所悬挂物体的最大重力是多少?
 如图所示,能承受最大拉力为100N的细线OA与竖直方向成45°角,能承受最大拉力为5 0N的细线OB水平,细线OC能承受足够大的拉力,为使OA,OB均不被拉断,OC下端所悬挂物体的最大重力是多少?
如图所示,能承受最大拉力为100N的细线OA与竖直方向成45°角,能承受最大拉力为5 0N的细线OB水平,细线OC能承受足够大的拉力,为使OA,OB均不被拉断,OC下端所悬挂物体的最大重力是多少?
12.如图所示,一金属半圆环置于匀强磁场中,当磁场突然减弱时,则两端点的电势( )


| A. | N点电势高 | |
| B. | M点电势高 | |
| C. | 若磁场不变,将半圆环绕MN轴旋转180°的过程中,N点电势高 | |
| D. | 若磁场不变,将半圆环绕MN轴旋转180°的过程中,M点电势高 |
2.下列物体运动的情况中,可能存在的是( )
| A. | 某时刻物体的加速度很大而速度为零 | |
| B. | 物体的速度大小不变但加速度不为零 | |
| C. | 物体的速度保持不变但其速率在增大 | |
| D. | 物体的速率在增大但加速度却为零 |
6.关于弹性势能和重力势能下列说法中不正确的是( )
| A. | 重力势能属于物体和地球这个系统,弹性势能属于发生弹性形变的物体 | |
| B. | 零势能的选择会影响某状态重力势能,但不影响一个过程中重力势能的改变 | |
| C. | 重力做正功时,重力势能减少;弹簧弹力做正功时,弹性势能增加 | |
| D. | 重力势能和弹性势能都是状态量 |
 如图所示,带电荷量为Q的正点电荷固定在倾角为30°的光滑绝缘斜面底部的C点,斜面上有A、B两点,且A、B和C在同一直线上,A和C相距为L,B为AC中点.现将一带电小球从A点由静止释放,当带电小球运动到B点时速度正好又为零,已知带电小球在A点处的加速度大小为$\frac{g}{4}$,静电力常量为k,求:
如图所示,带电荷量为Q的正点电荷固定在倾角为30°的光滑绝缘斜面底部的C点,斜面上有A、B两点,且A、B和C在同一直线上,A和C相距为L,B为AC中点.现将一带电小球从A点由静止释放,当带电小球运动到B点时速度正好又为零,已知带电小球在A点处的加速度大小为$\frac{g}{4}$,静电力常量为k,求: