题目内容
如图所示,一个长l=8m的传送带上表面距地面高度为h=0.2m,传送带以ν=6m/s的速度顺时针传动,传送带右端有一个斜面,斜面倾角θ=370,斜面底端通过一小段光滑圆弧和传送带相连,圆弧处放置一个小物块C,不计物块C由传送带滑上斜面过程的能量损失,且物块C与斜面间的动摩擦因数μ1=0.25.有两个可视为质点且靠紧的小物块A和B,A、B之间夹有少量炸药,把A、B放在传送带左端的同时引爆炸药,炸药瞬间爆炸,A物体水平向左抛出,落地点距传送带左端水平距离s=0.9m,B物体在传送带上运动,与传送带间的动摩擦因数μ2=0.2,已知mA=1kg,mB=mc=0.5kg,已知sin37°=0.6,cos37°=0.8,求:
(1)炸药爆炸后B物体的速度.
(2)从炸药爆炸到B第一次离开传送带,物块B与传送带因摩擦而产生的热量Q
(3)若B、C相碰交换速度,从炸药爆炸到B最后离开传送带的过程中传送带对B所做的总功.

(1)炸药爆炸后B物体的速度.
(2)从炸药爆炸到B第一次离开传送带,物块B与传送带因摩擦而产生的热量Q
(3)若B、C相碰交换速度,从炸药爆炸到B最后离开传送带的过程中传送带对B所做的总功.
分析:(1)根据平抛运动的规律求出A的初速度,结合动量守恒定律求出炸药爆炸后B物体的速度.
(2)通过计算判断出B在传送带上的运动情况,结合运动学公式求出B的相对运动位移的大小,从而求出摩擦产生的热量.
(3)通过动能定理判断出B停止的位置,从而求出炸药爆炸到B最后离开传送带的过程中传送带对B所做的总功.
(2)通过计算判断出B在传送带上的运动情况,结合运动学公式求出B的相对运动位移的大小,从而求出摩擦产生的热量.
(3)通过动能定理判断出B停止的位置,从而求出炸药爆炸到B最后离开传送带的过程中传送带对B所做的总功.
解答:解:(1)A物体做平抛,水平方向:s=vAt
竖直方向上h=
gt2
解得t=0.2s,vA=4.5m/s.
炸药爆炸过程中A、B动量守恒,有:mAvA=mBvB,解得vB=9m/s.
(2)设物体B在传送带上一直减速,加速度a=
=μ2g=2m/s2
B到达C处的速度为v1,有2aL=vB2-v12,解得v1=7m/s.
因为v1>v,所以B一直减速,运行时间t1=
=1s.
B与传送带因摩擦而产生的热量Q=μ2mBg(L-vt)
解得Q=2J.
(3)物体B、C交换速度后B静止,C以v1滑上斜面,设上滑s1,根据动能定理得,
-μ1mcgcos37°?s1-mcgsin37°?s1=0-
mcv12
解得s1=2.45m
设C滑回底端时的速度为v2,根据动能定理有:
-μ1mcgcos37°?s1+mcgsin37°?s1=
mcv22-0
B与C交换速度后C静止,B滑上传送带,B从左端离开传送带需克服摩擦力做功
Wf=μ2mBgL
代入数据解得
mBv22<μ2mBgL
因此B不会离开传送带,最终静止于C处,传送带对B所做的总功
W=-μ2mBgL=-8J
答:(1)炸药爆炸后B物体的速度为9m/s.
(2)从炸药爆炸到B第一次离开传送带,物块B与传送带因摩擦而产生的热量为2J.
(3)若B、C相碰交换速度,从炸药爆炸到B最后离开传送带的过程中传送带对B所做的总功为-8J.
竖直方向上h=
| 1 |
| 2 |
解得t=0.2s,vA=4.5m/s.
炸药爆炸过程中A、B动量守恒,有:mAvA=mBvB,解得vB=9m/s.
(2)设物体B在传送带上一直减速,加速度a=
| μ2mBg |
| mB |
B到达C处的速度为v1,有2aL=vB2-v12,解得v1=7m/s.
因为v1>v,所以B一直减速,运行时间t1=
| vB-v1 |
| a |
B与传送带因摩擦而产生的热量Q=μ2mBg(L-vt)
解得Q=2J.
(3)物体B、C交换速度后B静止,C以v1滑上斜面,设上滑s1,根据动能定理得,
-μ1mcgcos37°?s1-mcgsin37°?s1=0-
| 1 |
| 2 |
解得s1=2.45m
设C滑回底端时的速度为v2,根据动能定理有:
-μ1mcgcos37°?s1+mcgsin37°?s1=
| 1 |
| 2 |
B与C交换速度后C静止,B滑上传送带,B从左端离开传送带需克服摩擦力做功
Wf=μ2mBgL
代入数据解得
| 1 |
| 2 |
因此B不会离开传送带,最终静止于C处,传送带对B所做的总功
W=-μ2mBgL=-8J
答:(1)炸药爆炸后B物体的速度为9m/s.
(2)从炸药爆炸到B第一次离开传送带,物块B与传送带因摩擦而产生的热量为2J.
(3)若B、C相碰交换速度,从炸药爆炸到B最后离开传送带的过程中传送带对B所做的总功为-8J.
点评:本题综合考查了动量守恒定律,动能定理、功能关系,综合性较强,对学生的能力要求较高,需加强训练.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,用长L=0.50m的绝缘轻质细线,把一个质量m=1.0g带电小球悬挂在带等量异种电荷的平行金属板之间,平行金属板间的距离d=5.0cm,两板间电压U=1.0×103V.静止时,绝缘线偏离竖直方向θ角,小球偏离竖直距离a=1.0cm.(θ角很小,为计算方便可认为tanθ≈sinθ,取g=10m/s2,需要求出具体数值,不能用θ角表示)求:
如图所示,用长L=0.50m的绝缘轻质细线,把一个质量m=1.0g带电小球悬挂在带等量异种电荷的平行金属板之间,平行金属板间的距离d=5.0cm,两板间电压U=1.0×103V.静止时,绝缘线偏离竖直方向θ角,小球偏离竖直距离a=1.0cm.(θ角很小,为计算方便可认为tanθ≈sinθ,取g=10m/s2,需要求出具体数值,不能用θ角表示)求: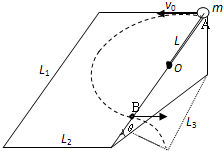 如图所示,一个长L1=0.9m、宽L2=0.6m的光滑斜面体,其倾角θ=30°.有一长度L=0.4m的轻质绳一端固定在距斜面顶点A为L=0.4m斜面边缘的O点上,另一端系一质量m=1kg的小球.现把小球拉至顶点A处,以v0=1m/s的初速度沿斜面顶边缘水平抛出.(g取10m/s2)
如图所示,一个长L1=0.9m、宽L2=0.6m的光滑斜面体,其倾角θ=30°.有一长度L=0.4m的轻质绳一端固定在距斜面顶点A为L=0.4m斜面边缘的O点上,另一端系一质量m=1kg的小球.现把小球拉至顶点A处,以v0=1m/s的初速度沿斜面顶边缘水平抛出.(g取10m/s2) 如图所示,一个长为L=1m、质量M=2kg,厚度可以忽略不计的木板B静止在水平地面上,一个质量为m=3kg的物块A(可视为质点)从B的左端以速度v0=3m/s的初速度向右滑上木板B.若A、B与水平地面的摩擦因数均为μ1=0.2,A、B之间的动摩擦因数为μ2=0.4,求:
如图所示,一个长为L=1m、质量M=2kg,厚度可以忽略不计的木板B静止在水平地面上,一个质量为m=3kg的物块A(可视为质点)从B的左端以速度v0=3m/s的初速度向右滑上木板B.若A、B与水平地面的摩擦因数均为μ1=0.2,A、B之间的动摩擦因数为μ2=0.4,求: