题目内容
17.月球的公转周期是1个月,同步卫星的公转周期是一天.二者相比( )| A. | 月球运行的线速度比同步卫星大 | |
| B. | 月球运行的角速度比同步卫星大 | |
| C. | 月球运行的向心加速度比同步卫星小 | |
| D. | 月球的轨道半径比同步卫星小 |
分析 卫星绕地球圆周运动的向心力由万有引力提供,$G\frac{Mm}{{r}_{\;}^{2}}$=mω2r=m$\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,根据周期关系得出半径关系,再展开讨论即可.
解答 解:根据万有引力提供向心力,有$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}=m{ω}_{\;}^{2}r=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,得$v=\sqrt{\frac{GM}{r}}$,$ω=\sqrt{\frac{GM}{{r}_{\;}^{3}}}$,$T=2π\sqrt{\frac{{r}_{\;}^{3}}{GM}}$,$a=\frac{GM}{{r}_{\;}^{2}}$
D、根据题意,月球的周期大于同步卫星的公转周期,所以月球的轨道半径大于同步卫星的轨道半径,故D错误;
A、由$v=\sqrt{\frac{GM}{r}}$知,月球的轨道半径大,所以月球的线速度较小,故A错误;
B、根据$ω=\sqrt{\frac{GM}{{r}_{\;}^{3}}}$,因为月球的轨道半径较大,所以月球运行的角速度较小,故B错误;
C、根据$a=\frac{GM}{{r}_{\;}^{2}}$,因为月球的轨道半径大,所以月球的向心加速度较小,故C正确;
故选:C
点评 在万有引力应用中,对于卫星问题应牢记万有引力提供向心力,解决问题的核心是$G\frac{Mm}{{r}_{\;}^{2}}$=mω2r=$m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列说法正确的是( )
| A. | 天然放射性现象说明原子核内部具有复杂的结构 | |
| B. | α粒子散射实验说明原子核内部具有复杂的结构 | |
| C. | 原子核发生α衰变生成的新核原子序数增加 | |
| D. | 氢原子从能级3跃迁到能级2辐射出的光子的波长小于从能级2跃迁到能级1辐射出的光子的波长 |
5.我国计划在2017年12月发射“嫦娥五号”探测器,主要是完成月面取样返回任务,设探测器在离月面高度为h的轨道上绕月做匀速圆周运动时,周期为T,已知月球表面重力加速度为g0,月球半径为R,万有引力常量为G,根据以上信息可求出( )
| A. | 探测器绕月运行的速度为$\frac{2πR}{T}$ | B. | 月球的第一宇宙速度为$\sqrt{R{g}_{0}}$ | ||
| C. | 月球的质量为$\frac{{R}^{2}{g}_{0}}{G}$ | D. | 月球的平均密度为$\frac{3π}{G{T}^{2}}$ |
12. 在半球形光滑碗内,斜放一根筷子,如图所示,筷子与碗的接触点分别为A、B,则碗对筷子A、B两点处的作用力方向分别为( )
在半球形光滑碗内,斜放一根筷子,如图所示,筷子与碗的接触点分别为A、B,则碗对筷子A、B两点处的作用力方向分别为( )
 在半球形光滑碗内,斜放一根筷子,如图所示,筷子与碗的接触点分别为A、B,则碗对筷子A、B两点处的作用力方向分别为( )
在半球形光滑碗内,斜放一根筷子,如图所示,筷子与碗的接触点分别为A、B,则碗对筷子A、B两点处的作用力方向分别为( )| A. | A点处指向球心O,B点处竖直向上 | |
| B. | 均竖直向上 | |
| C. | A点处指向球心O,B点处垂直于筷子斜向上 | |
| D. | 均指向球心O |
9.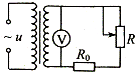 如图所示,理想变压器原、副线圈的匝数比为11:2,原线圈两端的输入正弦交流电压B表达式u=220$\sqrt{2}$sin100πt(V),副线圈两端所接的电压表为理想电压表,定值电阻R0=10Ω,滑动变阻器R的阻值变化范围为0~20Ω,下列说法正确的是( )
如图所示,理想变压器原、副线圈的匝数比为11:2,原线圈两端的输入正弦交流电压B表达式u=220$\sqrt{2}$sin100πt(V),副线圈两端所接的电压表为理想电压表,定值电阻R0=10Ω,滑动变阻器R的阻值变化范围为0~20Ω,下列说法正确的是( )
 如图所示,理想变压器原、副线圈的匝数比为11:2,原线圈两端的输入正弦交流电压B表达式u=220$\sqrt{2}$sin100πt(V),副线圈两端所接的电压表为理想电压表,定值电阻R0=10Ω,滑动变阻器R的阻值变化范围为0~20Ω,下列说法正确的是( )
如图所示,理想变压器原、副线圈的匝数比为11:2,原线圈两端的输入正弦交流电压B表达式u=220$\sqrt{2}$sin100πt(V),副线圈两端所接的电压表为理想电压表,定值电阻R0=10Ω,滑动变阻器R的阻值变化范围为0~20Ω,下列说法正确的是( )| A. | 电压表的示数为40V | |
| B. | 副线圈输出电压的频率为50Hz | |
| C. | 滑动变阻器R消耗功率的最大值为20W | |
| D. | 滑动变阻器滑片向下移动,变压器的输出功率不变 |
3. 如图所示,光滑水平面上存有界匀强磁场,磁感应强度为B,质量为m边长为a的正方形线框ABCD斜向穿进磁场,当AC刚进入磁场时速度为v,方向与磁场边界成45°,若线框的总电阻为R,则( )
如图所示,光滑水平面上存有界匀强磁场,磁感应强度为B,质量为m边长为a的正方形线框ABCD斜向穿进磁场,当AC刚进入磁场时速度为v,方向与磁场边界成45°,若线框的总电阻为R,则( )
 如图所示,光滑水平面上存有界匀强磁场,磁感应强度为B,质量为m边长为a的正方形线框ABCD斜向穿进磁场,当AC刚进入磁场时速度为v,方向与磁场边界成45°,若线框的总电阻为R,则( )
如图所示,光滑水平面上存有界匀强磁场,磁感应强度为B,质量为m边长为a的正方形线框ABCD斜向穿进磁场,当AC刚进入磁场时速度为v,方向与磁场边界成45°,若线框的总电阻为R,则( )| A. | 线框穿进磁场过程中,框中电流的方向为DCBA | |
| B. | AC刚进入磁场时线框中感应电流表为$\frac{{\sqrt{2}Bav}}{R}$ | |
| C. | AC刚进入磁场时线框所受安培力为$\frac{{\sqrt{2}{B^2}{a^2}v}}{R}$ | |
| D. | 此时CD两端电压为$\frac{3}{4}Bav$ |