题目内容
4.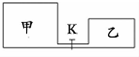 如图所示,装有同种理想气体的甲乙两个容器之间由细管相连.开始时阀门k关闭.甲中气体的体积为2V,压强为3P,温度为T,乙中气体的体积为V,压强为P,温度为T.现打开阀门,直至达到重新平衡,且温度保持不变.求:
如图所示,装有同种理想气体的甲乙两个容器之间由细管相连.开始时阀门k关闭.甲中气体的体积为2V,压强为3P,温度为T,乙中气体的体积为V,压强为P,温度为T.现打开阀门,直至达到重新平衡,且温度保持不变.求:(1)重新平衡时,容器中的气体压强?
(2)甲容器中的气体流出质量和原有气体质量的比?
分析 (1)根据对A、B两部分气体分别运用玻意耳定律求末态压强
(2)对A气体根据玻意耳定律求出末态体积,再求流出质量和原有质量之比
解答 解:①阀门打开后,气体由甲容器流入乙容器,直到两容器的气体压强相等.设甲气体的初状态为:${P}_{1}^{\;}=3P$,${V}_{1}^{\;}=2V$,${T}_{1}^{\;}=T$;末状态为:${p}_{2}^{\;}$,${V}_{2}^{\;}=3V$,${T}_{2}^{\;}=T$
由于温度不变,根据玻意耳定律得:${p}_{1}^{\;}{V}_{1}^{\;}={p}_{2}^{\;}{V}_{2}^{\;}$
解得:=$\frac{{p}_{1}^{\;}{V}_{1}^{\;}}{{V}_{2}^{\;}}=2p$
设乙气体的初状态为:${p}_{3}^{\;}=p$,${V}_{3}^{\;}=V$,${T}_{3}^{\;}=T$;末状态为:${p}_{4}^{\;}$,${V}_{4}^{\;}=3V$,${T}_{4}^{\;}=T$
由于温度不变,根据玻意耳定律得:${p}_{3}^{\;}{V}_{3}^{\;}={p}_{4}^{\;}{V}_{4}^{\;}$
解得:${p}_{4}^{\;}=\frac{{p}_{3}^{\;}{V}_{3}^{\;}}{{V}_{4}^{\;}}=\frac{p}{3}$
所以,重新平衡时,容器中的气体压强为$p={p}_{2}^{\;}+{p}_{4}^{\;}=2p+\frac{1}{3}p=\frac{7}{3}p$
②甲气体的第三状态为:${p}_{5}^{\;}=\frac{7}{3}p$,${V}_{5}^{\;}$,${T}_{5}^{\;}=T$
由于温度不变,根据玻意耳定律得${p}_{1}^{\;}{V}_{1}^{\;}={p}_{5}^{\;}{V}_{5}^{\;}$
解得:${V}_{5}^{\;}=\frac{{p}_{1}^{\;}{V}_{1}^{\;}}{{p}_{5}^{\;}}=\frac{18}{7}V$
甲容器中的气体流出量和原有气体质量的比:$\frac{{V}_{5}^{\;}-{V}_{1}^{\;}}{{V}_{5}^{\;}}=\frac{\frac{18}{7}V-2V}{\frac{18}{7}V}=\frac{2}{9}$
答:(1)重新平衡时,容器中的气体压强$\frac{7}{3}p$
(2)甲容器中的气体流出质量和原有气体质量的比$\frac{2}{9}$
点评 本题考查了求气体的压强,考查了气体实验定律的应用,本题是一道连接体问题,本题难度较大,巧妙选择研究对象是解题的关键,求出气体的状态参量、应用理想气体状态方程可以解题;解题时要注意各研究对象状态参量间的关系.

| A. | 甲队与地面的摩擦力大于乙队与地面的摩擦力 | |
| B. | 甲队拉绳子的力大于乙队拉绳子的力 | |
| C. | 甲队与地面摩擦力的大小等于乙队与地面摩擦力的大小 | |
| D. | 甲队拉绳子力的大小等于乙队拉绳子力的大小 |
 一个圆盘可绕通过圆盘中心O且垂直与盘面的竖直轴转动.在圆盘上放置材质相同的小木块甲、乙、丙,质量分别为m、2m、2m,它们随圆盘一起作匀速圆周运动,小木块甲、乙、丙距离O点的距离分别问r、r、2r.当圆盘转动角速度逐渐缓慢增大时,最先滑动的木块是( )
一个圆盘可绕通过圆盘中心O且垂直与盘面的竖直轴转动.在圆盘上放置材质相同的小木块甲、乙、丙,质量分别为m、2m、2m,它们随圆盘一起作匀速圆周运动,小木块甲、乙、丙距离O点的距离分别问r、r、2r.当圆盘转动角速度逐渐缓慢增大时,最先滑动的木块是( )| A. | 甲先滑动 | B. | 乙先滑动 | ||
| C. | 丙先滑动 | D. | 甲和乙一起先滑动 |
| A. | 单分子油膜的厚度被认为等于油分子的直径 | |
| B. | 实验时先将一滴油酸酒精溶液滴入水面,再把痱子粉洒在水面上 | |
| C. | 实验中数油膜轮廓内的正方形格数时,不足一格的应全部舍去 | |
| D. | 处理数据时将一滴油酸酒精溶液的体积除以油膜面积就算得油酸分子的直径 |
 某弹簧振子在水平方向上做简谐运动,其位移x随时间t变化的关系为x=A sinωt,振动图象如图所示,下列说法不正确的是( )
某弹簧振子在水平方向上做简谐运动,其位移x随时间t变化的关系为x=A sinωt,振动图象如图所示,下列说法不正确的是( )| A. | 弹簧在第1s末与第3s末的长度相同 | |
| B. | 简谐运动的角速度ω=$\frac{π}{4}$rad/s | |
| C. | 第3s末振子的位移大小为$\frac{\sqrt{2}}{2}$A | |
| D. | 从第3s末到第5s末,振子的速度方向发生变化 |
| A. | 封闭在容器内的液体很难被压缩,证明分子间有斥力 | |
| B. | 温度相同的氢气和氧气,氢气分子和氧气分子的平均速率相同 | |
| C. | 夏天荷叶上小水珠呈球状,是由于液体表面张力使其表面积具有收缩到到最小趋势的缘故 | |
| D. | 自然界中进行的一切与热现象有关的宏观过程都具有方向性 |
 如图所示是某居住小区门口利用光敏电阻设计的行人监控装置,R1为光敏电阻,R2为定值电阻,A,B接监控装置.则( )
如图所示是某居住小区门口利用光敏电阻设计的行人监控装置,R1为光敏电阻,R2为定值电阻,A,B接监控装置.则( )| A. | 当有人通过而遮蔽光线时,A,B之间电压升高 | |
| B. | 当有人通过而遮蔽光线时,A,B之间电压降低 | |
| C. | 当仅增大R1的阻值时,可增大A,B之间的电压 | |
| D. | 当仅减少R2的阻值时,可增大A,B之间的电压 |
 “验证动量守恒定律”的实验装置如图所示.让质量为m1的A小球从斜面上某处自由滚下与静止在支柱上质量为m2的B小球发生对心碰撞,则:
“验证动量守恒定律”的实验装置如图所示.让质量为m1的A小球从斜面上某处自由滚下与静止在支柱上质量为m2的B小球发生对心碰撞,则: