Question

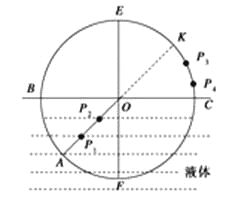
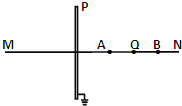
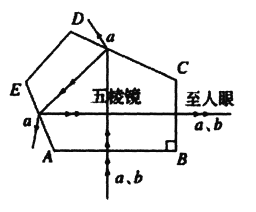
【题目】如图，质量均为m的两个小球A、B固定在弯成直角的绝缘轻杆两端，AB=OB=l，可绕过O点且与纸面垂直的水平轴无摩擦地在竖直平面内转动，空气阻力不计。A球带正电，B球带负电，电量均为q，整个系统处在竖直向下的匀强电场中，场强E=。开始时，AB水平，以图中AB位置为重力势能和电势能的零点，问：

(1)为使系统在图示位置平衡，需在A点施加一力F，则F至少多大？方向如何？

(2)若撤去F，OB转过45°角时，A球角速度多大？此时系统电势能总和是多大？

(3)若撤去F，OB转过多大角度时，系统机械能最大？最大值是多少？

Answer 1

【答案】（1）；方向与AB成角斜向上（2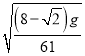）；（3）90°；

【解析】

(1)当垂直于时力最小，根据力矩平衡：

已知：

可以求出：

方向与成角斜向上

(2)对系统列动能定理可得：

其中：

，

可得：

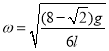
此时，电场力对球做正功，则有：

电场力对球做负功，则有：

则电场力对系统做功：

则系统电势能：

(3)电势能最小时，机械能最大，由(2)的结论，系统电势能总和为：

即当，电势能最小：

初始位置时，电势能和机械能均为零，则此时最大机械能：