题目内容
如图所示，圆心在O点、半径为R的圆弧支架竖直放置，支架底边ab离地距离为4R，Oc与Oa夹角为60°，圆弧边缘c处有一小滑轮，圆弧边缘a处切线水平；一轻绳两端系着质量分别为m1和m2的小球，挂在定滑轮两边。开始时，m1和m2均静止，且都可视为质点，不计一切摩擦，
求：①为使m1能够沿圆弧下滑到a点，m1和m2之间必须满足什么关系（连线足够长，此时m2没有到达c点）？
②已知m1=3m2，若m1到达圆弧最低点a时（此时m2没有到达c点），绳子恰好与m1断开，则m1落地点离a点的水平距离是多少？
⑴为使m1能够沿圆弧下滑到a点，则m1滑到a点时的速度恰好为零。
由m1和m2组成的系统机械能守恒
∴
（4分）
∴
即：
时，可使m1能够沿圆弧下滑到a点 （2分）
⑵由速度分解，v2=v1cos30° （2分）
由m1和m2组成的系统机械能守恒
（4分）
得
（1分）
由平抛运动可知
（2分）
（2分）
解析:
略
练习册系列答案
相关题目
（2013?徐汇区一模）如图所示，圆心在O点、半径为R的光滑圆弧轨道ABC竖直固定在水平桌面上，OC与OA的夹角为60°，轨道最低点A与桌面相切．一足够长的轻绳两端分别系着质量为m1和m2的两小球（均可视为质点），挂在圆弧轨道光滑边缘C的两边，开始时m1位于C点，然后从静止释放．则（ ）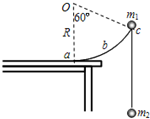
如图所示，圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上，Oc与Oa的夹角为60°，轨道最低点a与桌面相切．一轻绳两端系着质量为m1和m2的小球（均可视为质点），挂在圆弧轨道边缘c的两边，开始时，m1位于c点，然后从静止释放，设轻绳足够长，不计一切摩擦．则（ ）
（2013?龙江县二模）如图所示，圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上，Oc与Oa的夹角为60°，轨道最低点a与桌面相切．一轻绳两端系着质量为m1和m2的小球（均可视为质点），挂在圆弧轨道边缘c的两边，开始时，m1位于c点，然后从静止释放，设轻绳足够长，不计一切摩擦．则（ ）
如图所示，圆心在O点，半径为R=0.24m的圆弧形支架abc竖直固定在水平桌面上，支架最低点a与桌面相切，最高点c与O点的连线Oc与Oa夹角为60°．一轻绳两端系着质量分别为m1和m2的小球A和B（均可视为质点），挂在圆弧边缘c的两边．开始时，A、B均静止，A的位置与c点等高，不计一切摩擦，连线和水平桌面足够长，g=10m/s2．