题目内容
20. 如图,在半径为R圆环圆心O正上方的P点,将一小球以速度v0水平抛出后恰能从圆环上Q点沿切线飞过,若OQ与OP间夹角为θ,不计空气阻力.则( )
如图,在半径为R圆环圆心O正上方的P点,将一小球以速度v0水平抛出后恰能从圆环上Q点沿切线飞过,若OQ与OP间夹角为θ,不计空气阻力.则( )| A. | 从P点运动到Q点的时间为t=$\frac{Rsinθ}{v_0}$ | |
| B. | 从P点运动到Q点的时间为t=$\frac{Rcosθ}{v_0}$ | |
| C. | 小球运动到Q点时的速度为vQ=$\frac{v_0}{sinθ}$ | |
| D. | 小球运动到Q点时的速度为vQ=$\frac{v_0}{cosθ}$ |
分析 小球做平抛运动,根据圆的几何知识可以求得小球在水平方向的位移的大小,根据水平方向的匀速直线运动可以求得时间的大小.根据平行四边形定则求出Q点的速度.
解答 解:A、过Q点做OP的垂线,根据几何关系可知,小球在水平方向上的位移的大小为Rsinθ,
根据Rsinθ=v0t,
可得时间为:t=$\frac{Rsinθ}{{v}_{0}}$,故A正确,B错误.
C、根据几何关系知,Q点的速度方向与水平方向的夹角为θ,根据平行四边形定则知,小球运动到Q点时的速度为vQ=$\frac{{v}_{0}}{cosθ}$,故C错误,D正确.
故选:AD.
点评 本题对平抛运动规律的直接的应用,知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 物体的内能是物体所有分子热运动的动能和分子间的势能之和 | |
| B. | 布朗运动就是液体分子或者气体分子的热运动 | |
| C. | 气体分子间距离减小时,分子间斥力增大,引力减小 | |
| D. | 利用浅层海水和深层海水之间的温度差制造一种热机,将海水的一部分内能转化为机械能是可能的 | |
| E. | 一定量的理想气体,在压强不变时,分子每秒对器壁单位面积平均碰撞次数随着温度降低而增加 |
15. 如图所示,一台加湿器置于水平地面上,当加湿器水平向左喷出水汽时仍保持静止不动,下列判断正确的是( )
如图所示,一台加湿器置于水平地面上,当加湿器水平向左喷出水汽时仍保持静止不动,下列判断正确的是( )
 如图所示,一台加湿器置于水平地面上,当加湿器水平向左喷出水汽时仍保持静止不动,下列判断正确的是( )
如图所示,一台加湿器置于水平地面上,当加湿器水平向左喷出水汽时仍保持静止不动,下列判断正确的是( )| A. | 加湿器受到5个力作用 | B. | 加湿器受到6个力作用 | ||
| C. | 与加湿器有关的相互作用力有2对 | D. | 与加湿器有关的相互作用力有4对 |
5.在网络和报刊杂志中有很多介绍科技发展的文章,但有些文章存在物理单位使用或介绍错误的现象.以下四个单位中有三项使用或介绍错误,唯一正确的是( )
| A. | 发电地板亮相街头,…平均每个人从板上走过两次就可以产生0.5瓦的电能 | |
| B. | 特斯拉(Tesla)汽车得名于…,特斯拉也是国际单位制中磁通量的单位 | |
| C. | 神七航天员将穿着中国研制的舱外航天服出舱行走,…航天服内压力为40千帕 | |
| D. | 天文学家用三角测量学的方法,…计算出牛郎星与织女星的距离为16光年 |
 如图所示,在xOy平面内,以O1(0,R)为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B1,x轴下方有一直线ab,ab与x轴相距为d,x轴与直线ab间区域有平行于y轴的匀强电场E,在ab的下方有一平行于x轴的感光板MN,ab与MN间区域有垂直于纸平面向外的匀强磁场B2.
如图所示,在xOy平面内,以O1(0,R)为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B1,x轴下方有一直线ab,ab与x轴相距为d,x轴与直线ab间区域有平行于y轴的匀强电场E,在ab的下方有一平行于x轴的感光板MN,ab与MN间区域有垂直于纸平面向外的匀强磁场B2.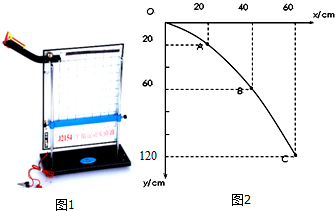
 质量为m=4kg的物块沿粗糙水平面运动,当物块运动到P处,其速度为15m/s,此时给物块施加一个与水平方向成53°,大小与物块运动速度大小v成反比的推力,如图所示.已知物块与水平面的动摩擦因数μ=0.75,推力大小F与速度大小v的关系为F=$\frac{50}{v}$(F单位为N,v单位为m•s-1)重力加速度g取10m/s2,sin53°=0.8,cos53°=0.6.
质量为m=4kg的物块沿粗糙水平面运动,当物块运动到P处,其速度为15m/s,此时给物块施加一个与水平方向成53°,大小与物块运动速度大小v成反比的推力,如图所示.已知物块与水平面的动摩擦因数μ=0.75,推力大小F与速度大小v的关系为F=$\frac{50}{v}$(F单位为N,v单位为m•s-1)重力加速度g取10m/s2,sin53°=0.8,cos53°=0.6.


 在“用DIS研究质量一定时,加速度与外力的关系”的实验中,某同学连接完如图所示的实验器材进行实验.
在“用DIS研究质量一定时,加速度与外力的关系”的实验中,某同学连接完如图所示的实验器材进行实验.