Question

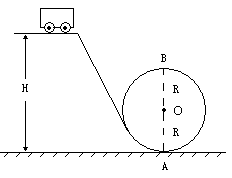
香港海洋公园的过山车建立在海拔120m的山坡上，如图所示，轨道总长为842m，每车可载28人，过山车以每小时80km(大约22.2m/s)的高速绕两个半径为5.25m的大圆环回旋，若有一乘客的质量为60kg，则他经过圆环的最低点A时对座椅的压力为多少？要保证过山车安全通过最高点B时，过山车至少从多高的地方下滑？

Answer 1

答案：
解析：

巧解分析：乘客通过最低点对底座的压力可用圆周运动的知识求解；而要保证过山车安全通过最高点B点，则在最高点必须满足临界条件：即对底座的压力必须大于零，或重力至少要提供向心力． 　　(1)当过山车在圆环的最低点A时，乘客受到重力G和座椅的支持力N作用，这两个力的合力是乘客做圆周运动的向心力，根据向心力公式，得NA－mg＝m，解得座椅对乘客的支持力为NA＝mg＋m＝5976N． 　　根据牛顿第三定律可知乘客对座椅的压力为＝5976N(方向竖直向下)． 　　(2)当过山车在圆环的最高点B时，乘客受到重力G和座椅的支持力N作用，根据向心力公式得：NB＋mg＝m，要过山车安全通过最高点B，必须满足NB≥0，即vB≥， 　　设过山车从高为H的地方开始下滑，根据动能定理，得mg(H－2R)＝m， 　　解得H＞R＝13.75m，由于圆环与过山车之间有摩擦力，所以过山车的高度为H＞13.75m．

提示：

命题意图：本题考查竖直平面的圆周运动知识和牛顿运动定律．