题目内容
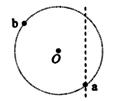
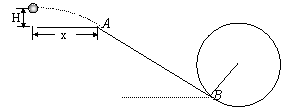
如图，一半径为R=1m的光滑圆形轨道竖直放置，一倾角为θ=370的粗糙斜面与圆形轨道相切，斜面上端为平台并与圆形轨道最高点等高，斜面动摩擦因素为μ=0.75，一人在平台上距斜面上端A点水平距离为x处以一定的初速度水平抛出一质量为m=1kg的物体（可看着质点），设抛出点高度为H，要使物体刚好能沿与斜面AB相切的速度由A点切入斜面，则：
（1）写出H、x应满足的关系式？
（2）要使物体能通过圆弧最高点，物体抛出时的高度H应多大？ (sin370=0.6, cos370=0.8, g取10m／s2)
 |
（1）
（2）斜面高
最高点速度
从A点到轨道最高点，由动能定理得
代入数据得H=0.828m
练习册系列答案
相关题目
（2013?太原一模）如图，一半径为R的圆表示一柱形区域的横截面（纸面）．在柱形区域内加一方向垂直于纸面向外的匀强磁场，磁感应强度大小为B．一质量为m、电荷量为q的带正电粒子以某一初速度v0（未知）从a点沿直径aOb方向射入柱形区域（磁场），从圆上的C点离开该区域，已知Oc与Ob成60°角，回答下列问题：
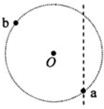如图，一半径为R的圆表示一柱形区域的横截面（纸面）．在柱形区域内加一方向垂直于纸面的匀强磁场，一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域，在圆上的b点离开该区域，离开时速度方向与直线垂直．圆心O到直线的距离为| 1 |
| 2 |
A、v=
| ||||
B、v=
| ||||
C、v=
| ||||
D、v=
|
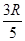。现将磁场换为平行于纸面且垂直于直线的匀强电场，同一粒子以同样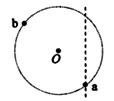
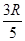。现将磁场换为平行于纸面且垂直于直线的匀强电场，同一粒子以同样