题目内容
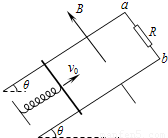
如图所示,固定的光滑金属导轨间距为L,导轨电阻不计,上端a、b间接有阻值为R的电阻,导轨平面与水平面的夹角为θ,且处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中.质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行.(1)求初始时刻通过电阻R的电流I的大小和方向;
(2)当导体棒第一次回到初始位置时,速度变为v,求此时导体棒的加速度大小a;
(3)导体棒最终静止时弹簧的弹性势能为Ep,求导体棒从开始运动直到停止的过程中,电阻R上产生的焦耳热Q.
【答案】分析:(1)棒向上运动切割磁感线,由E1=BLv求感应电动势,由欧姆定律求感应电流,根据右手定则判断感应电流的方向;
(2)当导体棒第一次回到初始位置时,速度变为v,棒产生的感应电动势为E2=BLv,再由欧姆定律求得感应电流,由F=BIL求出此时棒所受的安培力,根据牛顿第二定律就可以求出加速度;
(3)导体棒最终静止时,由胡克定律求出弹簧的被压缩长度x,对整个过程,运用能量守恒列式,可求出回路产生的总热量,再串联关系求出R上产生的焦耳热Q.
解答:解: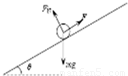
(1)棒产生的感应电动势E1=BLv
通过R的电流大小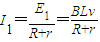
根据右手定则判断得知:电流方向为b→a
(2)棒产生的感应电动势为E2=BLv
感应电流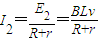
棒受到的安培力大小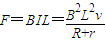 ,方向沿斜面向上,如图所示.
,方向沿斜面向上,如图所示.
根据牛顿第二定律 有 mgsinθ-F=ma
解得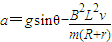
(3)导体棒最终静止,有 mgsinθ=kx
弹簧的压缩量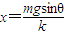
设整个过程回路产生的焦耳热为Q,根据能量守恒定律 有
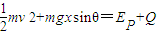
解得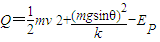
电阻R上产生的焦耳热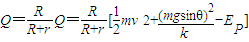
答:
(1)初始时刻通过电阻R的电流I的大小为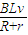 ,方向为b→a;
,方向为b→a;
(2)此时导体棒的加速度大小a为gsinθ-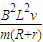 ;
;
(3)导体棒从开始运动直到停止的过程中,电阻R上产生的焦耳热Q为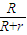 [
[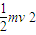 +
+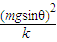 -EP].
-EP].
点评:本题是导体棒在导轨上滑动的类型,分析、计算安培力和分析能量如何转化是解题的关键,综合性较强.
(2)当导体棒第一次回到初始位置时,速度变为v,棒产生的感应电动势为E2=BLv,再由欧姆定律求得感应电流,由F=BIL求出此时棒所受的安培力,根据牛顿第二定律就可以求出加速度;
(3)导体棒最终静止时,由胡克定律求出弹簧的被压缩长度x,对整个过程,运用能量守恒列式,可求出回路产生的总热量,再串联关系求出R上产生的焦耳热Q.
解答:解:

(1)棒产生的感应电动势E1=BLv
通过R的电流大小
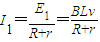
根据右手定则判断得知:电流方向为b→a
(2)棒产生的感应电动势为E2=BLv
感应电流
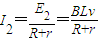
棒受到的安培力大小
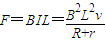 ,方向沿斜面向上,如图所示.
,方向沿斜面向上,如图所示.根据牛顿第二定律 有 mgsinθ-F=ma
解得
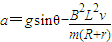
(3)导体棒最终静止,有 mgsinθ=kx
弹簧的压缩量
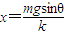
设整个过程回路产生的焦耳热为Q,根据能量守恒定律 有
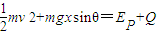
解得
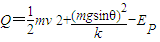
电阻R上产生的焦耳热
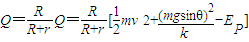
答:
(1)初始时刻通过电阻R的电流I的大小为
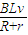 ,方向为b→a;
,方向为b→a;(2)此时导体棒的加速度大小a为gsinθ-
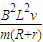 ;
;(3)导体棒从开始运动直到停止的过程中,电阻R上产生的焦耳热Q为
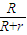 [
[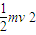 +
+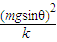 -EP].
-EP].点评:本题是导体棒在导轨上滑动的类型,分析、计算安培力和分析能量如何转化是解题的关键,综合性较强.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图所示,固定的光滑斜面上,重力为G的物体在一水平推力F作用下处于静止状态.若斜面的倾角为θ,则( )
如图所示,固定的光滑斜面上,重力为G的物体在一水平推力F作用下处于静止状态.若斜面的倾角为θ,则( )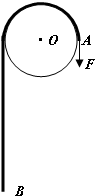 如图所示,固定的光滑圆柱体半径R=
如图所示,固定的光滑圆柱体半径R= 如图所示,固定的光滑竖直杆上套着一个滑块,滑块用轻绳系着绕过光滑的定滑轮O;现以大小不变的拉力F拉绳,使滑块从A点起由静止开始上升,运动到C点时速度达最大.已知:滑块质量为m,滑轮O到竖直杆的距离为d,∠OAO=37°、∠OCO=53°;求:
如图所示,固定的光滑竖直杆上套着一个滑块,滑块用轻绳系着绕过光滑的定滑轮O;现以大小不变的拉力F拉绳,使滑块从A点起由静止开始上升,运动到C点时速度达最大.已知:滑块质量为m,滑轮O到竖直杆的距离为d,∠OAO=37°、∠OCO=53°;求: 如图所示,固定的光滑倾斜杆上套有一个质量为m的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A 点,开始弹簧恰好处于原长h.现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为g.则在圆环下滑的整个过程中( )
如图所示,固定的光滑倾斜杆上套有一个质量为m的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A 点,开始弹簧恰好处于原长h.现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为g.则在圆环下滑的整个过程中( ) 如图所示,固定的光滑圆弧轨道ACB的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m.物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2.若物块从A点下滑到传送带上后,又恰能返回到C点,
如图所示,固定的光滑圆弧轨道ACB的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m.物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2.若物块从A点下滑到传送带上后,又恰能返回到C点,