题目内容
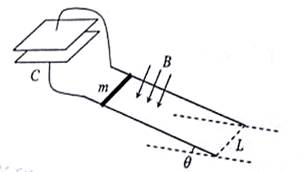
如图，两条平行导轨所在平面与水平地面的夹角为θ，间距为L。导轨上端接有一平行板电容器，电容为C。导轨处于匀强磁场中，磁感应强度大小为B，方向垂直于导轨平面。在导轨上放置一质量为m的金属棒，棒可沿导轨下滑，且在下滑过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ，重力加速度大小为g。忽略所有电阻。让金属棒从导轨上端由静止开始下滑，求:
(1)电容器极板上积累的电荷量与金属棒速度大小的关系；
(2)金属棒的速度大小随时间变化的关系。
解（1）设金属棒下滑的速度大小为v，则感应电动势为
①
平行板电容器两极板之间的电势差为U=E ②
设此时电容器极板上积累的电荷量为Q，按定义有
③
联立①②③式得 
④
（2）设金属棒的速度大小为v时经历的时间为t，通过金属棒的电流为i。金属棒受到的磁场的作用力方向沿导轨向上，大小为
⑤
设在时间间隔（t，t+Δt）内流经金属棒的电荷量为ΔQ，按定义有
⑥
ΔQ也是平行板电容器极板在时间间隔（t，t+Δt）内增加的电荷量。由4式得
⑦
式中Δv为金属棒的速度变化量，按定义有
⑧
金属棒所受到的摩擦力方向斜向上，大小为
⑨
式中N是金属棒对导轨的正压力的大小，有
⑩
金属棒在时刻t的加速度方向沿斜面向下，设其大小为a，根据牛顿第二定律有
联立⑤至11式得
由上式及题设可知，金属棒做初速度为零的匀加速运动，t时刻金属棒的速度大小为
练习册系列答案
相关题目
（2005?衡阳模拟）电磁炮的基本原理如图所示，把待发射的炮弹（导体）放置在强磁场中的两条平行导轨（导轨与水平方向成α角）上，磁场方向和导轨平面垂直，若给导轨以很大的电流I，使用权炮弹作为一个载流导体在磁场的作用下，沿导轨作加速运动，以某一速度发射出去，已知匀强磁场的磁感应强度为B，两导轨间的距离为L，磁场中导轨的长度为S，炮弹的质量为m，炮弹和导轨间摩擦以及炮弹本身的长度均不计，试求炮弹离开炮口时的速度．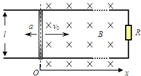
如图，两条互相平行且足够长的光滑金属导轨位于水平面内，导轨间距l=0.2m，在导轨的
如图所示，同一水平面上的两条平行导轨ab、cd置于竖直向上的匀强磁场中，间距为2m．一根质量为2kg的金属棒PQ垂直两导轨放置，金属棒与导轨间的动摩擦因数为0.2．当金属棒中通入5A的电流时，金属棒向右加速运动，加速度大小为2m/s2，取g=lOm/s2．求磁感应强度的大小和金属棒PQ中电流的方向．
电磁炮是利用电磁发射技术制成的一种先进的动能杀伤武器，它的主要原理如图所示，把待发射的炮弹（导体）放置在处于匀强磁场中的两条平行导轨上，给导轨通以电流，使炮弹作为一个载流导体在磁场的作用下，沿导轨作加速运动（此过程视为匀加速运动），以某一速度发射出去．1982年澳大利亚国立大学制成了能把2.2g的弹体（也包括金属杆EF的质量）加速到10km/s的电磁炮，若导轨宽为2m，长为100m，不计摩擦，通过的电流为10A．则：