题目内容
11. 光滑的半圆形竖直轨道,其圆心与墙在同一竖直平面内,轨道的下端与水平相切,水平面高出地面H=2R,如图所示,一小球沿水平方向进入半圆形轨道下端,小球沿轨道运动的过程中对轨道的压力的大小和小球与圆心的连线同竖直方向的夹角θ满足关系式F=k+kcosθ,其中k为常数,求:
光滑的半圆形竖直轨道,其圆心与墙在同一竖直平面内,轨道的下端与水平相切,水平面高出地面H=2R,如图所示,一小球沿水平方向进入半圆形轨道下端,小球沿轨道运动的过程中对轨道的压力的大小和小球与圆心的连线同竖直方向的夹角θ满足关系式F=k+kcosθ,其中k为常数,求:(1)常数k的大小;
(2)小球落地点到竖直墙的水平距离L.
分析 (1)对圆弧上任一点分析,由向心力公式及动能定理可得出F的表达式,则由求得K值;
(2)对全程由动能定理及平抛运动规律可求得水平距离.
解答 解:在圆弧上任取一点A,对小球在A点受力分析,由向心力公式可得:F-mgcosθ=m$\frac{{v}_{A}^{2}}{R}$
对从最低点到A过程,由动能定理可得:
-mgR(1-cosθ)=$\frac{1}{2}$mvA2-$\frac{1}{2}$mv02
联立解得:
F=$\frac{m{v}_{0}^{2}}{R}-2mg+3mgcosθ$
由题意可知:
F=k+kcosθ
故k=$\frac{m{v}_{0}^{2}}{R}$-2mg=3mg
故可知:k=3mg;
v0=$\sqrt{5gR}$
(2)从最低点到最高点,由动能定理可得:
-2mgR=$\frac{1}{2}$mvB2-$\frac{1}{2}$mv02
解得:vB=$\sqrt{gR}$
由平抛运动规律可知:
H+2R=$\frac{1}{2}$gt2
x=vBt
解得:x=2$\sqrt{2}$R
答:(1)常数k的大小为$\sqrt{5gR}$;
(2)小球落地点到竖直墙的水平距离为2$\sqrt{2}$R.
点评 本题考查动能定理、平抛运动规律和向心力公式,要求能明确通式的书写,并正确应用平抛及向心力公式等于分析求解.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
1.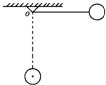 一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速释放小球.如图所示,小球从开始运动至轻绳达竖直位置的过程中,小球重力的瞬时功率的变化情况是( )
一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速释放小球.如图所示,小球从开始运动至轻绳达竖直位置的过程中,小球重力的瞬时功率的变化情况是( )
 一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速释放小球.如图所示,小球从开始运动至轻绳达竖直位置的过程中,小球重力的瞬时功率的变化情况是( )
一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速释放小球.如图所示,小球从开始运动至轻绳达竖直位置的过程中,小球重力的瞬时功率的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大,后减小 | D. | 先减小,后增大 |
2.下列说法正确的是( )
| A. | 卢瑟福通过实验发现了质子的核反应方程为${\;}_{2}^{4}$He+${\;}_{7}^{14}$N→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H | |
| B. | 铀核裂变的核反应是:${\;}_{92}^{235}$U→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$O+2${\;}_{0}^{1}$n | |
| C. | 太阳源源不断的释放出巨大的能量,其能量的来涿就是太阳本身的核裂变 | |
| D. | 现在的很多手表指针上涂有一种新型发光材料,白天吸收光子外层电子跃迁到高能轨道,晚上向低能级跃迁放出光子,其发光的波长一定跟吸收的光的波长完全一致 | |
| E. | 光电效应现象说明光具有粒子性 | |
| F. | 卢瑟福首先发现了天然放射现象,说明原子核还有复杂的结构 |
19.以下说法正确的是( )
| A. | 金刚石、食盐、玻璃和水晶都是晶体 | |
| B. | 飘浮在热菜汤表面上的油滴,从上面的观察是圆形的,是因为油滴液体呈各向同性的缘故 | |
| C. | 对于一定量的理想气体,外界对气体做功,气体内能可能减少 | |
| D. | 扩散运动就是布朗运动 |
16.如图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1m处的质点,Q是平衡位置为x=4m处的质点,图乙为质点Q的振动图象,则( )


| A. | t=0.15s时,质点Q的加速度等于零 | |
| B. | t=0.15s时,质点P的运动方向沿Y轴负方向 | |
| C. | 从t=0.10s,到t=0.25s,该波沿X轴正方向传播了6m | |
| D. | 从t=0.10s到t=0.25s,质点P通过的路程为30cm |
3. 负点电荷Q固定在正方形的一个顶点上,带电粒子仅在该点电荷的电场力作用下运动时,恰好能经过正方形的另外三个顶点a、b、c,如图所示,则下列说法错误的是( )
负点电荷Q固定在正方形的一个顶点上,带电粒子仅在该点电荷的电场力作用下运动时,恰好能经过正方形的另外三个顶点a、b、c,如图所示,则下列说法错误的是( )
 负点电荷Q固定在正方形的一个顶点上,带电粒子仅在该点电荷的电场力作用下运动时,恰好能经过正方形的另外三个顶点a、b、c,如图所示,则下列说法错误的是( )
负点电荷Q固定在正方形的一个顶点上,带电粒子仅在该点电荷的电场力作用下运动时,恰好能经过正方形的另外三个顶点a、b、c,如图所示,则下列说法错误的是( )| A. | 粒子P带负电 | |
| B. | a、b、c三点的电势高低关系是φa=φc<φb | |
| C. | 粒子P由a到b电势能增加,由b到c电势能减小 | |
| D. | 粒子P在a、b、三点时的加速度大小之比是2:1:2 |
12. 如图所示,一个矩形线框从匀强磁场的上方自由落下,进入匀强磁场中后,再从磁场中穿出.匀强磁场区域的宽度L大于线框的高度h.已知线框的下边刚进入磁场时线框的加速度为零,空气阻力不计.则下列说法正确的是( )
如图所示,一个矩形线框从匀强磁场的上方自由落下,进入匀强磁场中后,再从磁场中穿出.匀强磁场区域的宽度L大于线框的高度h.已知线框的下边刚进入磁场时线框的加速度为零,空气阻力不计.则下列说法正确的是( )
 如图所示,一个矩形线框从匀强磁场的上方自由落下,进入匀强磁场中后,再从磁场中穿出.匀强磁场区域的宽度L大于线框的高度h.已知线框的下边刚进入磁场时线框的加速度为零,空气阻力不计.则下列说法正确的是( )
如图所示,一个矩形线框从匀强磁场的上方自由落下,进入匀强磁场中后,再从磁场中穿出.匀强磁场区域的宽度L大于线框的高度h.已知线框的下边刚进入磁场时线框的加速度为零,空气阻力不计.则下列说法正确的是( )| A. | 从线框开始运动到线框下边刚进入磁场前的过程中,重力所做的功完全转化为线框的动能 | |
| B. | 从线框下边刚进入磁场到线框刚好全部进入磁场的过程中,重力所做的功完全转化为线框同路的电能 | |
| C. | 线框完全在磁场中运动的过程中,重力所做的功完全转化为线框的动能 | |
| D. | 线框穿出磁场的过程中,重力所做的功完全转化为线框的动能 |
 如图所示,粗细均匀,两端开口的U形管竖直放置,管的内径很小,水平部分BC长14cm,一空气柱将管内水银分隔成左右两段,大气压强相当于高为76cm水银柱的压强.
如图所示,粗细均匀,两端开口的U形管竖直放置,管的内径很小,水平部分BC长14cm,一空气柱将管内水银分隔成左右两段,大气压强相当于高为76cm水银柱的压强. A、B两小车的质量均为M,在光滑水平面上相向而行,速度大小均为1.8m/s,A车内有一质量为$\frac{M}{4}$的小球C.用长L=0.4m的细线悬挂在车厢顶上并相对于车厢静止,如图所示.若A、B在极短时间内相撞并连接在一起.求:
A、B两小车的质量均为M,在光滑水平面上相向而行,速度大小均为1.8m/s,A车内有一质量为$\frac{M}{4}$的小球C.用长L=0.4m的细线悬挂在车厢顶上并相对于车厢静止,如图所示.若A、B在极短时间内相撞并连接在一起.求: