题目内容
如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子,从y轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.求
(1)在原图上画出粒子在电场和磁场中运动轨迹示意图;
(2)电场强度大小E;
(3)粒子在磁场中运动的轨道半径r;
(4)粒子从进入电场到离开磁场经历的总时间t.
(1)在原图上画出粒子在电场和磁场中运动轨迹示意图;
(2)电场强度大小E;
(3)粒子在磁场中运动的轨道半径r;
(4)粒子从进入电场到离开磁场经历的总时间t.


(1)类似平抛运动速度偏转角的正切:tanθ=2tanα=2×
| y |
| x |
故粒子的运动轨迹如右图所示;
(2)设粒子在电场中运动的时间为t1
x方向:2h=v0t1
y方向:h=
| 1 |
| 2 |
根据牛顿第二定律:Eq=ma
联立以上三式,解得:E=
m
| ||
| 2qh |
故电场强度为
m
| ||
| 2qh |
(3)类平抛运动过程,根据动能定理:Eqh=
| 1 |
| 2 |
| 1 |
| 2 |
将E的表达式代入上式,得:v=
| 2 |
由:Bqv=m
| v2 |
| r |
得:r=
| ||
| Bq |
故圆弧的半径为
| ||
| Bq |
(4)粒子在电场中运动的时间:t1=
| 2h |
| v0 |
粒子在磁场中运动的周期:T=
| 2πr |
| v |
| 2πm |
| Bq |
根据粒子入射磁场时与x轴成45°,射出磁场时垂直于y轴,可求出粒子在磁场中运动的圆弧所对的圆心角为135°.
故粒子在磁场中运动的时间为:t2=
| 3 |
| 8 |
求出 t=t1+t2=
| 2h |
| v0 |
| 3πm |
| 4Bq |
故粒子的运动时间为
| 2h |
| v0 |
| 3πm |
| 4Bq |
答:(1)粒子的运动轨迹如右图所示;
(2)电场强度为
m
| ||
| 2qh |
(3)圆弧的半径为
| ||
| Bq |
(4)粒子的运动时间为
| 2h |
| v0 |
| 3πm |
| 4Bq |

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
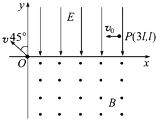 如图所示,在平面直角坐标xOy内,第I象限有沿一y方向的匀强电场,第IV象限有垂直于纸面向外的匀强磁场.现有一质量为m、带电量为+q的粒子(重力不计)以初速度v0沿-x方向从坐标为(3l,l)的P点开始运动,接着进人磁场后由坐标原点O射出,射出时速度方向与y轴方向夹角为45°,求
如图所示,在平面直角坐标xOy内,第I象限有沿一y方向的匀强电场,第IV象限有垂直于纸面向外的匀强磁场.现有一质量为m、带电量为+q的粒子(重力不计)以初速度v0沿-x方向从坐标为(3l,l)的P点开始运动,接着进人磁场后由坐标原点O射出,射出时速度方向与y轴方向夹角为45°,求 如图所示,直角坐标平面xOy内有一条直线AC过坐标原点O与x轴成45°夹角,在OA与x轴负半轴之间的区域内存在垂直xOy平面向外的匀强磁场B,在OC与x轴正半轴之间的区域内存在垂直xOy平面向外的匀强磁场B2.现有一质量为m,带电量为q(q>0)的带电粒子以速度v从位于直线AC上的P点,坐标为(L,L),竖直向下射出,经测量发现,此带电粒子每经过相同的时间T,会再将回到P点,已知距感应强度
如图所示,直角坐标平面xOy内有一条直线AC过坐标原点O与x轴成45°夹角,在OA与x轴负半轴之间的区域内存在垂直xOy平面向外的匀强磁场B,在OC与x轴正半轴之间的区域内存在垂直xOy平面向外的匀强磁场B2.现有一质量为m,带电量为q(q>0)的带电粒子以速度v从位于直线AC上的P点,坐标为(L,L),竖直向下射出,经测量发现,此带电粒子每经过相同的时间T,会再将回到P点,已知距感应强度
