��Ŀ����
 ��ͼ��ʾ��ֱ������ƽ��xOy����һ��ֱ��AC������ԭ��O��x���45��нǣ���OA��x�Ḻ����֮��������ڴ��ڴ�ֱxOyƽ���������ǿ�ų�B����OC��x��������֮��������ڴ��ڴ�ֱxOyƽ���������ǿ�ų�B2������һ����Ϊm��������Ϊq��q��0���Ĵ����������ٶ�v��λ��ֱ��AC�ϵ�P�㣬����Ϊ��L��L������ֱ������������������֣��˴�������ÿ������ͬ��ʱ��T�����ٽ��ص�P�㣬��֪���Ӧǿ��B2=
��ͼ��ʾ��ֱ������ƽ��xOy����һ��ֱ��AC������ԭ��O��x���45��нǣ���OA��x�Ḻ����֮��������ڴ��ڴ�ֱxOyƽ���������ǿ�ų�B����OC��x��������֮��������ڴ��ڴ�ֱxOyƽ���������ǿ�ų�B2������һ����Ϊm��������Ϊq��q��0���Ĵ����������ٶ�v��λ��ֱ��AC�ϵ�P�㣬����Ϊ��L��L������ֱ������������������֣��˴�������ÿ������ͬ��ʱ��T�����ٽ��ص�P�㣬��֪���Ӧǿ��B2=| mv |
| qL |
��1������ͼ�л����������ӵ��˶��켣���������ǿ�ų�B1��B2�ı�ֵ����B1��B2�ų��㹻��
��2��������������������ξ���P���ʱ����T��
��3�������ִŸ�Ӧǿ��B2���䣬�ı�B1�Ĵ�С�������ı��䷽��ʹB1=
| mv |
| 2qL |
| v |
| 4 |
| v |
| 3 |
��4����Ҫʹ��3������˵��������������ͬʱ�����ξ���ֱ��AC�������������ӵ�һ�δ�P�����ʱ��ʱ������tҪ���
��������1�������ڴų���������Բ���˶������������ṩ������������ţ�ٵڶ�������ʽ������뾶�������������ֱ���˶��������켣��
��2������t=
?T��T=
����Բ���˶���ʱ�䣬����������ֱ���˶���ʱ�����Ӽ��ɣ�
��3������������Բ���˶������������ṩ������������ţ�ٵڶ����������뾶֮��Ĺ�ϵ��Ȼ����Ӧ�Ĺ켣���õ�EF��ࣻ
��4��������������ͬһ�ų��е�������ͬ��ת����Բ�Ľ�Ҳ��ͬ������ͬһ�ų��е��˶�ʱ����ͬ������ʱ������t����ֱ���˶���ʱ��
��2������t=
| �� |
| 2�� |
| 2��m |
| qB |
��3������������Բ���˶������������ṩ������������ţ�ٵڶ����������뾶֮��Ĺ�ϵ��Ȼ����Ӧ�Ĺ켣���õ�EF��ࣻ
��4��������������ͬһ�ų��е�������ͬ��ת����Բ�Ľ�Ҳ��ͬ������ͬһ�ų��е��˶�ʱ����ͬ������ʱ������t����ֱ���˶���ʱ��
��� �⣺��1���������Ӵ�P�������˶���Q�㣬Ȼ�����뾶Ϊ��qvB2=m
�⣺��1���������Ӵ�P�������˶���Q�㣬Ȼ�����뾶Ϊ��qvB2=m
?R2=
=L������Բ���˶����˶���H��ʱ���ٶȷ�����AC��ֱ����H�������˶���D�㣬��������Բ���˶���P�㣮
����ƽ�漸��֪ʶ��֪��
=
=
L���ı���AODOR1RΪ���Σ�OR1RΪԲ�ģ���������������ǿ�ų�BR1R��������Բ���˶�ʱ�İ뾶RR1RΪ
L������qvB1=m
��
�ã�B1=
=
B2��
��2��T=t1+t2+t3+t4
t1=
��
t2=
T2=
��
t3=
��
t4=
T2=
��ã�T=t1+t2+t3+t4=
��
��3�������������ڴų�BR2R���˶�ʱ�İ뾶Ϊ��R��2=
=
��
R��2=
=
B1=
=
��
�������ڴų�BR1R�е��˶��뾶��
R1=
=2R2��
�����������Ӷ��պ��˶�
Բ�ܵ���A�㣬����EF�����ľ���EF=0����ͼ��ʾ����
��4��������������ͬһ�ų��е�������ͬ��ת����Բ�Ľ�Ҳ��ͬ������ͬһ�ų��е��˶�ʱ����ͬ������ʱ������t����ֱ���˶���ʱ��
��t=
-
=
��
�𣺣�1���������ӵ��˶��켣��ͼ��ʾ����ǿ�ų�B1��B2�ı�ֵΪ
��
��2�����������������ξ���P���ʱ����TΪ
��
��3��EF�����ľ���Ϊ0��
��4�����������ӵ�һ�δ�P�����ʱ��ʱ������tΪ
��
 �⣺��1���������Ӵ�P�������˶���Q�㣬Ȼ�����뾶Ϊ��qvB2=m
�⣺��1���������Ӵ�P�������˶���Q�㣬Ȼ�����뾶Ϊ��qvB2=m| v2 |
| R2 |
| mv |
| qB2 |
����ƽ�漸��֪ʶ��֪��
. |
| PO |
. |
| OD |
| 2 |
| 2 |
| v2 |
| R1 |
�ã�B1=
| ||
| 2qL |
| ||
| 2 |
��2��T=t1+t2+t3+t4
t1=
| L |
| v |
t2=
| 3 |
| 8 |
| 3��L |
| 4v |
t3=
| L |
| v |
t4=
| 5 |
| 8 |
5
| ||
| 4v |
��ã�T=t1+t2+t3+t4=
(8+3��+5
| ||
| 4v |
��3�������������ڴų�BR2R���˶�ʱ�İ뾶Ϊ��R��2=
m
| ||
| qB2 |
| L |
| 4 |
R��2=
m
| ||
| qB2 |
| L |
| 3 |
B1=
| mv |
| 2qL |
| B2 |
| 2 |
�������ڴų�BR1R�е��˶��뾶��
R1=
| mv |
| qB1 |
�����������Ӷ��պ��˶�
| 1 |
| 4 |
��4��������������ͬһ�ų��е�������ͬ��ת����Բ�Ľ�Ҳ��ͬ������ͬһ�ų��е��˶�ʱ����ͬ������ʱ������t����ֱ���˶���ʱ��
��t=
L+
| ||
|
L+
| ||
|
| 2L |
| v |
�𣺣�1���������ӵ��˶��켣��ͼ��ʾ����ǿ�ų�B1��B2�ı�ֵΪ
| ||
| 2 |
��2�����������������ξ���P���ʱ����TΪ
(8+3��+5
| ||
| 4v |
��3��EF�����ľ���Ϊ0��
��4�����������ӵ�һ�δ�P�����ʱ��ʱ������tΪ
| 2L |
| v |
����������ؼ���ȷ���ӵ��˶����ʣ������˶��켣��Ȼ�������Բ���˶���ֱ���˶������ۣ�

��ϰ��ϵ�д�
�����Ŀ
 �ڡ��о�ƽ��������˶�����ʵ���У�
�ڡ��о�ƽ��������˶�����ʵ���У�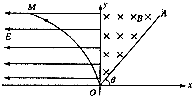 ��ͼ��ʾ����ֱ������ƽ��ĵ�I��������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB��ֱ��OA�Ǵų��Ҳ�ı߽磮�ڵڢ����������ڵ糡ǿ�ȴ�СΪE��ˮƽ�������ǿ�糡��y���ǵ糡���ų�����ķֽ������ߣ�OM���㷽��x=-ky2��k��0������һ�������Ϊq������Ϊm�ĸ����ӣ��������ƣ�������OM��ijһ���ɾ�ֹ�ͷţ���Խy�����ų��У�
��ͼ��ʾ����ֱ������ƽ��ĵ�I��������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB��ֱ��OA�Ǵų��Ҳ�ı߽磮�ڵڢ����������ڵ糡ǿ�ȴ�СΪE��ˮƽ�������ǿ�糡��y���ǵ糡���ų�����ķֽ������ߣ�OM���㷽��x=-ky2��k��0������һ�������Ϊq������Ϊm�ĸ����ӣ��������ƣ�������OM��ijһ���ɾ�ֹ�ͷţ���Խy�����ų��У�

