题目内容
10. 如图所示,两个相同材料制成的靠静摩擦传动的轮A和轮B水平放置,两轮半径RA=2RB.当主动轮A匀速转动时,在A轮边缘上放置的小木块恰能相对静止在A轮边缘上.若将小木块放在B轮上,欲使木块相对B轮也静止,则木块距B轮转轴的最大距离为多少?(设最大静摩擦力等于滑动摩擦力)
如图所示,两个相同材料制成的靠静摩擦传动的轮A和轮B水平放置,两轮半径RA=2RB.当主动轮A匀速转动时,在A轮边缘上放置的小木块恰能相对静止在A轮边缘上.若将小木块放在B轮上,欲使木块相对B轮也静止,则木块距B轮转轴的最大距离为多少?(设最大静摩擦力等于滑动摩擦力)
分析 解决本题的关键是两轮边缘上接触的地方线速度相等,共轴它们的角速度相等.然后根据角速度和线速度半径之间关系等求解.
解答 解:如图所示,两轮边缘的线速度大小相等,两轮半径RA=2RB. 则由v=ωR得:2ωA=ωB,
则由v=ωR得:2ωA=ωB,
在A轮边缘上放置的小木块恰能相对静止在A轮边缘上.则有最大静摩擦力提供向心力.即为μmg=mω2RA,当木块放在B轮也静止,
则木块距B轮转轴的最大距离为R′B
则有:$μmg=m{{ω}_{B}}^{2}R{′}_{B}$
所以$R{′}_{B}=\frac{{R}_{B}}{2}$
答:木块距B轮转轴的最大距离为$\frac{{R}_{B}}{2}$
点评 描述圆周运动的物理量较多如线速度、角速度、向心加速度、周期、频率、转速等,明确各物理量之间的关系,是解题的关键.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
20.关于无线电广播过程,下列说法正确的是( )
| A. | 话筒将声音信号转变成电信号 | |
| B. | 每个电台都能使用任意频率的电磁波发射信号 | |
| C. | 接收机上的天线,直接接收来自广播台的声音信号 | |
| D. | 收音机上的“调谐”旋钮起到选台的作用 |
18.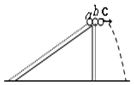 如图所示,a、b、c三个相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.下列说法正确的有( )
如图所示,a、b、c三个相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.下列说法正确的有( )
 如图所示,a、b、c三个相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.下列说法正确的有( )
如图所示,a、b、c三个相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.下列说法正确的有( )| A. | 它们的落地时间相同 | |
| B. | 落地时b、c两小球重力做功的瞬时功率相等 | |
| C. | 它们的落地时的动能相同 | |
| D. | 落地时a、b两小球重力做功的瞬时功率相等 |
5. 如图所示,等边三角形AOB为透明柱状介质的横截面.一束单色光PQ平行于角平分线OM射向OA,在界面OA发生折射,折射光线平行于OB且恰好射到M点(不考虑反射光线).则( )
如图所示,等边三角形AOB为透明柱状介质的横截面.一束单色光PQ平行于角平分线OM射向OA,在界面OA发生折射,折射光线平行于OB且恰好射到M点(不考虑反射光线).则( )
 如图所示,等边三角形AOB为透明柱状介质的横截面.一束单色光PQ平行于角平分线OM射向OA,在界面OA发生折射,折射光线平行于OB且恰好射到M点(不考虑反射光线).则( )
如图所示,等边三角形AOB为透明柱状介质的横截面.一束单色光PQ平行于角平分线OM射向OA,在界面OA发生折射,折射光线平行于OB且恰好射到M点(不考虑反射光线).则( )| A. | 透明柱状介质对单色光PQ的折射率为$\sqrt{3}$ | |
| B. | 增大入射光PQ的频率,光在该介质中的传播速度不变 | |
| C. | 保持入射点Q不变,减小入射角度,一直有光线从AMB面射出 | |
| D. | 保持入射光PQ的方向不变,增大入射光的频率,出射点将在M点下方 |
15.下列说法正确的是( )
| A. | ${\;}_{90}^{232}$Th经过6次α衰变和4次β衰变后成为稳定的原子核${\;}_{82}^{208}$Pb | |
| B. | 发现中子的核反应方程是${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+1n | |
| C. | 20个${\;}_{92}^{238}$U的原子核经过两个半衰期后剩下5个${\;}_{92}^{238}$U | |
| D. | 一定强度的入射光照射某金属发生光电效应时,入射光越强,单位时间内逸出的光电子数就越少 |
2.一物体做直线运动的v-t图象如图所示,可知合力对该物体( )


| A. | 做正功 | B. | 做负功 | ||
| C. | 先做正功后做负功 | D. | 先做负功后做正功 |
 如图所示,质量为M的木块置于光滑水平面上,一质量为m的子弹以水平速度v0打入木块并停在木块中,此过程中木块向前运动位移为XM,子弹打入木块深度为L,求:
如图所示,质量为M的木块置于光滑水平面上,一质量为m的子弹以水平速度v0打入木块并停在木块中,此过程中木块向前运动位移为XM,子弹打入木块深度为L,求: 如图所示,光滑水平面上有一木块,质量为M=1kg,长度1m.在木板的最左端有一个小滑块(可视为质点),质量为m=1kg.小滑块与木板之间的动摩擦因数μ=0.3.开始时它们都处于静止状态,某时刻起对小滑块施加一个F=8N水平向右的恒力,此后小滑块将相对于木板滑动,直到小滑块离开木板.g=10m/s2,求:
如图所示,光滑水平面上有一木块,质量为M=1kg,长度1m.在木板的最左端有一个小滑块(可视为质点),质量为m=1kg.小滑块与木板之间的动摩擦因数μ=0.3.开始时它们都处于静止状态,某时刻起对小滑块施加一个F=8N水平向右的恒力,此后小滑块将相对于木板滑动,直到小滑块离开木板.g=10m/s2,求: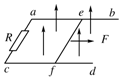 如图所示,abcd为静止于水平面上宽度为L而长度足够长的U型金属滑轨,ac边接有电阻R,其他部分电阻不计.ef为一可在滑轨平面上滑动、质量为m的均匀导体棒.整个滑轨面处在竖直向上的匀强磁场中,磁感应强度为B.忽略所有摩擦.若用恒力F沿水平方向向右拉棒,使其平动,求导体棒的最大速度.
如图所示,abcd为静止于水平面上宽度为L而长度足够长的U型金属滑轨,ac边接有电阻R,其他部分电阻不计.ef为一可在滑轨平面上滑动、质量为m的均匀导体棒.整个滑轨面处在竖直向上的匀强磁场中,磁感应强度为B.忽略所有摩擦.若用恒力F沿水平方向向右拉棒,使其平动,求导体棒的最大速度.