题目内容
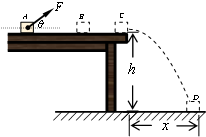
 如图所示,一滑块经水平轨道AB,进入竖直平面内的四分之一圆弧轨道BC,已知滑块的质量m=0.6kg,在A点的速度vA=8m/s,AB长x=5m,滑块与水平轨道间的动摩擦因数μ=0.15,圆弧轨道的半径R=2m,滑块离开C点后竖直上升h=0.2m,取g=10m/s2.求:
如图所示,一滑块经水平轨道AB,进入竖直平面内的四分之一圆弧轨道BC,已知滑块的质量m=0.6kg,在A点的速度vA=8m/s,AB长x=5m,滑块与水平轨道间的动摩擦因数μ=0.15,圆弧轨道的半径R=2m,滑块离开C点后竖直上升h=0.2m,取g=10m/s2.求:(1)滑块经过B点时速度的大小;
(2)滑块在圆弧轨道BC段克服摩擦力所做的功.
分析:(1)滑块由A至B过程,只有摩擦力做功,可以由动能定理求解;
(2)先根据运动学公式求出在C点的速度,再对滑块由B至C段过程运用动能定理列式求解;也可以直接对由B至最高点过程运用动能定理列式求解.
(2)先根据运动学公式求出在C点的速度,再对滑块由B至C段过程运用动能定理列式求解;也可以直接对由B至最高点过程运用动能定理列式求解.
解答:解:(1)滑块从A到B过程,只有摩擦力做功,由动能定理得
-fx=
mvB2-
mvA2
其中摩擦力 f=μmg
联立上式,解得
vB=7.0m/s
即滑块经过B点时速度的大小为7.0m/s.
(3)滑块离开C点后做竖直上抛运动,由运动学公式
vC2=2gh
从B到C的过程中,设摩擦力做功Wf,由动能定理
-mgR+wf=
mvC2-
vB2
解得 Wf=-1.5J
克服摩擦力做功Wf′=1.5J
即滑块在圆弧轨道BC段克服摩擦力所做的功为1.5J.
答(1)滑块经过B点时速度的大小是7.0m/s;
(2)滑块在圆弧轨道BC段克服摩擦力所做的功是1.5J..
-fx=
| 1 |
| 2 |
| 1 |
| 2 |
其中摩擦力 f=μmg
联立上式,解得
vB=7.0m/s
即滑块经过B点时速度的大小为7.0m/s.
(3)滑块离开C点后做竖直上抛运动,由运动学公式
vC2=2gh
从B到C的过程中,设摩擦力做功Wf,由动能定理
-mgR+wf=
| 1 |
| 2 |
| 1 |
| 2 |
解得 Wf=-1.5J
克服摩擦力做功Wf′=1.5J
即滑块在圆弧轨道BC段克服摩擦力所做的功为1.5J.
答(1)滑块经过B点时速度的大小是7.0m/s;
(2)滑块在圆弧轨道BC段克服摩擦力所做的功是1.5J..
点评:本题中第一问也可以根据运动学公式求解,但用动能定理求解不用考虑加速度,过程明显简化;运用动能定理要注意过程的选择,通常运动过程选的越大,解题过程越简化;动能定理比运动学公式适用范围更广,对于曲线运动同样适用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2008?北京)有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失.碰后B运动的轨迹为OD曲线,如图所示.
(2008?北京)有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失.碰后B运动的轨迹为OD曲线,如图所示.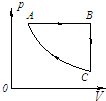
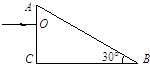
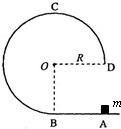 如图所示,在竖直平面内有一固定轨道,其中AB是长为R的粗糙水平直轨道,BCD是圆心为O、半径为R的3/4光滑圆弧轨道,两轨道相切于B点.在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C.重力加速度大小为g.则小滑块( )
如图所示,在竖直平面内有一固定轨道,其中AB是长为R的粗糙水平直轨道,BCD是圆心为O、半径为R的3/4光滑圆弧轨道,两轨道相切于B点.在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C.重力加速度大小为g.则小滑块( )