题目内容
Kˉ介子衰变的方程为K-→π-+π，如图所示，其中Kˉ介子和πˉ介子带负的基元电荷，π介子不带电．一个Kˉ介子沿垂直于磁场的方向射入匀强磁场中，其轨迹为圆弧AP，衰变后产生的πˉ介子的轨迹为圆弧PB，两轨迹在P点相切，它们的半径RKˉ与Rπ-之比为2：1．π介子的轨迹未画出．由此可知πˉ介子的动量大小与π介子的动量大小之比为（ ）
A．1：1
B．1：2
C．1：3
D．1：6
【答案】分析：曲线运动中，粒子的速度方向沿着轨迹上该点的切线方向，又由于Kˉ介子衰变过程中，系统内力远大于外力，系统动量守恒，故可知衰变后，π-介子反向飞出，π介子沿原方向飞出，再根据介子做圆周运动的向心力由洛伦兹力提供，可以列式求出Kˉ介子与π-介子的动量之比，再结合动量守恒定律列式分析．
解答：解：Kˉ介子与π-介子均做匀速圆周运动，洛伦兹力提供向心力，有
eBv=m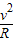
故动量
P=mv=eBR
因而
PKˉ：Pπ-=2：1
根据动量守恒定律，有
PKˉ=Pπ-Pπ-
故Pπ=3Pπ-
故选C．
点评：本题关键根据洛伦兹力提供向心力和动量守恒定律列式求解．
解答：解：Kˉ介子与π-介子均做匀速圆周运动，洛伦兹力提供向心力，有
eBv=m
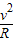
故动量
P=mv=eBR
因而
PKˉ：Pπ-=2：1
根据动量守恒定律，有
PKˉ=Pπ-Pπ-
故Pπ=3Pπ-
故选C．
点评：本题关键根据洛伦兹力提供向心力和动量守恒定律列式求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2003?天津）Kˉ介子衰变的方程为K-→π-+π0，如图所示，其中Kˉ介子和πˉ介子带负的基元电荷，π0介子不带电．一个Kˉ介子沿垂直于磁场的方向射入匀强磁场中，其轨迹为圆弧AP，衰变后产生的πˉ介子的轨迹为圆弧PB，两轨迹在P点相切，它们的半径RKˉ与Rπ-之比为2：1．π0介子的轨迹未画出．由此可知πˉ介子的动量大小与π0介子的动量大小之比为（ ）
（2013?河南模拟）K-介子衰变的方程为K-→π-+π0，其中K-介子和π-介子带负的元电荷e，π0介子不带电，π-介子的质量为m．如图所示，两匀强磁场方向相同，以虚线MN为理想边界，磁感应强度分别为B1、B2．今有一个
（1）下列说法正确的是：
与
之比为2∶1.π0介子的轨迹未画出.由此可知π-的动量大小与π0的动量大小之比为( ) 