题目内容
 如图所示,正方形线框的边长为L,从图示位置开始沿光滑斜面向下滑动,中途穿越垂直纸面向里、有理想边界的匀强磁场区域.磁场的宽度大于L,以i表示导线框中感应电流的大小,从线圈刚开始进入磁场时计时,取逆时针方向为电流的正方向.则以下四幅i-t关系图象,其中可能正确的是( )
如图所示,正方形线框的边长为L,从图示位置开始沿光滑斜面向下滑动,中途穿越垂直纸面向里、有理想边界的匀强磁场区域.磁场的宽度大于L,以i表示导线框中感应电流的大小,从线圈刚开始进入磁场时计时,取逆时针方向为电流的正方向.则以下四幅i-t关系图象,其中可能正确的是( )分析:由楞次定律判断感应电流方向.由法拉弟电磁感应定律、牛顿第二定律和运动学公式推导感应电流大小与位移的关系式,来选择图象.
解答:解:设导线框进入或穿出磁场时的瞬时速度为v,
导线框因切割磁感线而产生的感应电动势为:E=BLv,
感应电流i=
=
,
线框受到沿斜面向上的安培力大小为:F=BiL=
;
由右手定则可知,线框进入磁场时和穿出磁场时的感应电流的方向分别为沿逆时针方向(取正值)和顺时针方向(取负值);
①如果线框刚进入磁场时,安培力的大小满足:F=mgsinα,
线框将匀速进入磁场,感应电流i大小不变,所以i-t关系图象为平行于横轴的直线,
当线框完全进入磁场时,安培力为零,线框做匀加速直线运动;
当线框穿出磁场时,安培力F>mgsinα,线框做减速直线运动,因速度不断减小
所以安培力逐渐减小,线框的加速度a=
也不断减小,
即
不断减小,所以
=
不断减小,
又因为进出磁场位移相同,所以出磁场用时更短,B选项正确,AD选项错误.
②若线框刚进入磁场时,安培力F<mgsinα,线框做加速直线运动,因速度不断增大,所以安培力和感应电流均变大,线框的加速度a=
变小,i-t关系图象的斜率变小,如C项初始阶段的曲线所示.若线框穿出磁场时的感应电流减小,说明速度减小同前面分析过程,加速度减小,所以
=
不断减小,故C正确;
故选:BC.
导线框因切割磁感线而产生的感应电动势为:E=BLv,
感应电流i=
| E |
| R |
| BLv |
| R |
线框受到沿斜面向上的安培力大小为:F=BiL=
| B2L2v |
| R |
由右手定则可知,线框进入磁场时和穿出磁场时的感应电流的方向分别为沿逆时针方向(取正值)和顺时针方向(取负值);
①如果线框刚进入磁场时,安培力的大小满足:F=mgsinα,
线框将匀速进入磁场,感应电流i大小不变,所以i-t关系图象为平行于横轴的直线,
当线框完全进入磁场时,安培力为零,线框做匀加速直线运动;
当线框穿出磁场时,安培力F>mgsinα,线框做减速直线运动,因速度不断减小
所以安培力逐渐减小,线框的加速度a=
| F-mgsinα |
| m |
即
|
|
| BL |
| R |
|
又因为进出磁场位移相同,所以出磁场用时更短,B选项正确,AD选项错误.
②若线框刚进入磁场时,安培力F<mgsinα,线框做加速直线运动,因速度不断增大,所以安培力和感应电流均变大,线框的加速度a=
| mgsinα-F |
| m |
|
| BL |
| R |
|
故选:BC.
点评:图象往往由解析式选择.本题采用排除法,分成线性和非线性两类图象,对比同类图象的不同之处进行选择.

练习册系列答案
相关题目
 如图所示,正方形线框在F=21N的恒力作用下向上通过水平匀强磁场,磁场宽度h=1m,磁感应强度B=1T.线框边长L=1m,质量m=0.1kg,电阻R=1Ω,线框从1处由静止开始运动,当cd边刚进入磁场时线框恰好匀速,求线框从1位置开始运动到完全穿过磁场到达2位置的过程中,恒力F做的功和线框中产生的焦耳热分别是多少?(g取10m/s2)
如图所示,正方形线框在F=21N的恒力作用下向上通过水平匀强磁场,磁场宽度h=1m,磁感应强度B=1T.线框边长L=1m,质量m=0.1kg,电阻R=1Ω,线框从1处由静止开始运动,当cd边刚进入磁场时线框恰好匀速,求线框从1位置开始运动到完全穿过磁场到达2位置的过程中,恒力F做的功和线框中产生的焦耳热分别是多少?(g取10m/s2) (2011?唐山二模)如图所示,正方形线框的边长为L,从图示位置开始沿光滑斜面向下滑动.中途穿越垂直纸面向里,有理想边界的匀强磁场区域.磁场的宽度大于L,以i表示导线框中感应电流的强度,从线圈进入磁场开始计时,取逆时针方向为电流的正方向,在下列i-t关系图象中,可能正确的是( )
(2011?唐山二模)如图所示,正方形线框的边长为L,从图示位置开始沿光滑斜面向下滑动.中途穿越垂直纸面向里,有理想边界的匀强磁场区域.磁场的宽度大于L,以i表示导线框中感应电流的强度,从线圈进入磁场开始计时,取逆时针方向为电流的正方向,在下列i-t关系图象中,可能正确的是( ) (2004?惠州一模)如图所示,正方形线框abcd的总电阻为0.04Ω,质量为6.4g,边长为0.4m,用绝缘丝线竖直悬挂,其ab边水平,绝缘丝线的最大承受力为1N.图中两虚线之间是垂直于线框平面向里的匀强磁场,磁场上边界正好通过ad的bc有中点,磁感应强度从0.2T开始以0.1T/s的变化率均匀增大,问:
(2004?惠州一模)如图所示,正方形线框abcd的总电阻为0.04Ω,质量为6.4g,边长为0.4m,用绝缘丝线竖直悬挂,其ab边水平,绝缘丝线的最大承受力为1N.图中两虚线之间是垂直于线框平面向里的匀强磁场,磁场上边界正好通过ad的bc有中点,磁感应强度从0.2T开始以0.1T/s的变化率均匀增大,问: ,正方形线框 abcd 的总电阻为0.04Ω,质量为 6.4g,边长为0.4m,用绝缘丝线竖直悬挂,其 ab 边水平.图中两虚线之间是垂直于线框平面向里的匀强磁场,磁场上边界正好通过ac和bd的中点.磁感应强度从0.2T开始以0.1T/s的变化率均匀增大. 问:
,正方形线框 abcd 的总电阻为0.04Ω,质量为 6.4g,边长为0.4m,用绝缘丝线竖直悬挂,其 ab 边水平.图中两虚线之间是垂直于线框平面向里的匀强磁场,磁场上边界正好通过ac和bd的中点.磁感应强度从0.2T开始以0.1T/s的变化率均匀增大. 问: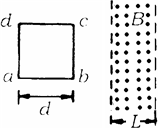 如图所示,正方形线框abcd的边长为d,向右通过宽为L的匀强磁场,且d>L,则在线框通过磁场的过程中,线框中的感应电流( )
如图所示,正方形线框abcd的边长为d,向右通过宽为L的匀强磁场,且d>L,则在线框通过磁场的过程中,线框中的感应电流( )