题目内容
 如图,光滑细杆组成一直角三角形AOB,竖立于一直角坐标系xOy中,OB边位于x轴上沿水平方向、AO边位于y轴上沿竖直方向,A点坐标为(0,8)、B点坐标为(6,0),OA及AB两边上分别套着用轻质弹性细线连结着的铜环P与Q.当它们均静止时,铜环P的位置坐标为(0,4),则铜环Q的横坐标可能范围为________<xQ<________.
如图,光滑细杆组成一直角三角形AOB,竖立于一直角坐标系xOy中,OB边位于x轴上沿水平方向、AO边位于y轴上沿竖直方向,A点坐标为(0,8)、B点坐标为(6,0),OA及AB两边上分别套着用轻质弹性细线连结着的铜环P与Q.当它们均静止时,铜环P的位置坐标为(0,4),则铜环Q的横坐标可能范围为________<xQ<________.
1.92 3
分析:本题可以运用假设法分析∠AQP与∠ABO的关系.假设P环和假设铜环Q的质量分别为零时,由平衡条件得到两环有质量时的角度的关系,再由几何知识求解铜环Q的横坐标可能范围.
解答:设∠AQP=θ,∠ABO=β.由数学知识得:tanβ=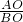 =
= ,得β=53°
,得β=53°
假设P环质量为零,重力为零,它仅受线的拉力和细杆AO的弹力,它们是一对平衡力.由于细杆对P环的弹力垂直于AO向左,则细线必定垂直于AO,则细线平行于BO,此时θ=β,此时Q的横坐标为x=APcotβ=4× =3.但实际上P环的质量大于零,重力大于零,要使此环处于静止,细线必须斜向右上方,则有θ>β,则Q有横坐标xQ<3.
=3.但实际上P环的质量大于零,重力大于零,要使此环处于静止,细线必须斜向右上方,则有θ>β,则Q有横坐标xQ<3.
假设铜环Q的质量为零,重力为零,它仅受细线的拉力和AB的弹力,它们是一对平衡力,则此环平衡时,细线与AB垂直,θ= ,此时Q的横坐标为x=APcos53°?sin53°=1.92.而实际是铜环Q的质量大于零,重力大于零,要使此环处于静止状态,细线不能与AB垂直,应有θ<
,此时Q的横坐标为x=APcos53°?sin53°=1.92.而实际是铜环Q的质量大于零,重力大于零,要使此环处于静止状态,细线不能与AB垂直,应有θ< ,故Q的横坐标应xQ>1.92.故铜环Q的横坐标可能范围为1.92<xQ<3.
,故Q的横坐标应xQ>1.92.故铜环Q的横坐标可能范围为1.92<xQ<3.
故答案为:1.92,3
点评:点评:本题运用假设法的思维方法,也可以通过分析两环的受力情况,由平衡条件,根据正交分解法确定θ的范围.
分析:本题可以运用假设法分析∠AQP与∠ABO的关系.假设P环和假设铜环Q的质量分别为零时,由平衡条件得到两环有质量时的角度的关系,再由几何知识求解铜环Q的横坐标可能范围.
解答:设∠AQP=θ,∠ABO=β.由数学知识得:tanβ=
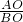 =
= ,得β=53°
,得β=53°假设P环质量为零,重力为零,它仅受线的拉力和细杆AO的弹力,它们是一对平衡力.由于细杆对P环的弹力垂直于AO向左,则细线必定垂直于AO,则细线平行于BO,此时θ=β,此时Q的横坐标为x=APcotβ=4×
 =3.但实际上P环的质量大于零,重力大于零,要使此环处于静止,细线必须斜向右上方,则有θ>β,则Q有横坐标xQ<3.
=3.但实际上P环的质量大于零,重力大于零,要使此环处于静止,细线必须斜向右上方,则有θ>β,则Q有横坐标xQ<3.假设铜环Q的质量为零,重力为零,它仅受细线的拉力和AB的弹力,它们是一对平衡力,则此环平衡时,细线与AB垂直,θ=
 ,此时Q的横坐标为x=APcos53°?sin53°=1.92.而实际是铜环Q的质量大于零,重力大于零,要使此环处于静止状态,细线不能与AB垂直,应有θ<
,此时Q的横坐标为x=APcos53°?sin53°=1.92.而实际是铜环Q的质量大于零,重力大于零,要使此环处于静止状态,细线不能与AB垂直,应有θ< ,故Q的横坐标应xQ>1.92.故铜环Q的横坐标可能范围为1.92<xQ<3.
,故Q的横坐标应xQ>1.92.故铜环Q的横坐标可能范围为1.92<xQ<3.故答案为:1.92,3
点评:点评:本题运用假设法的思维方法,也可以通过分析两环的受力情况,由平衡条件,根据正交分解法确定θ的范围.

练习册系列答案
相关题目
 如图所示,两固定光滑硬杆OA、OB组成夹角为O的支架,将支架水平放置,在两杆上各套一轻质环P、Q,两环用细绳相连.现用一大小为F的恒力沿OB方向拉圆环Q,当两环处于平衡状态时,OA杆对P环的弹力大小为
如图所示,两固定光滑硬杆OA、OB组成夹角为O的支架,将支架水平放置,在两杆上各套一轻质环P、Q,两环用细绳相连.现用一大小为F的恒力沿OB方向拉圆环Q,当两环处于平衡状态时,OA杆对P环的弹力大小为
 如图,光滑细杆组成一直角三角形AOB,竖立于一直角坐标系xOy中,OB边位于x轴上沿水平方向、AO边位于y轴上沿竖直方向,A点坐标为(0,8)、B点坐标为(6,0),OA及AB两边上分别套着用轻质弹性细线连结着的铜环P与Q.当它们均静止时,铜环P的位置坐标为(0,4),则铜环Q的横坐标可能范围为
如图,光滑细杆组成一直角三角形AOB,竖立于一直角坐标系xOy中,OB边位于x轴上沿水平方向、AO边位于y轴上沿竖直方向,A点坐标为(0,8)、B点坐标为(6,0),OA及AB两边上分别套着用轻质弹性细线连结着的铜环P与Q.当它们均静止时,铜环P的位置坐标为(0,4),则铜环Q的横坐标可能范围为