题目内容
如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道相距l=1m,两轨道之间用R=3Ω的电阻连接,一质量m=0.5kg、电阻r=1Ω的导体杆与两轨道垂直,静止放在轨道上,轨道的电阻可忽略不计.整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上,现用水平拉力沿轨道方向拉导体杆,拉力F与导体杆运动的位移s间的关系如图(乙)所示,当拉力达到最大时,导体杆开始做匀速运动,当位移s=2.5m时撤去拉力,导体杆又滑行了一段距离s'后停下,在滑行s'的过程中电阻R上产生的焦耳热为12J.求:
(1)拉力F作用过程中,通过电阻R上电量q;
(2)导体杆运动过程中的最大速度vm;
(3)拉力F作用过程中,电阻R上产生的焦耳热.
(1)拉力F作用过程中,通过电阻R上电量q;
(2)导体杆运动过程中的最大速度vm;
(3)拉力F作用过程中,电阻R上产生的焦耳热.

(1)拉力F作用过程中,在时间△t内,磁通量为△Φ,通过电阻R上电量q
q=
t
=
=
q=
=
=1.25 c
(2)导体杆先做加速运动,后匀速运动,撤去拉力后减速运动.设最大速度为vm
撤去F后金属棒滑行过程中动能转化为电能
∵
=
由能量守恒定律,得
=QR+Qr
∴vm=8m/s.
故导体杆运动过程中的最大速度为8m/s.
(2)匀速运动时最大拉力与安培力平衡
再分析匀速运动阶段,最大拉力为:
Fm=BIml=
vm=8N
拉力F作用过程中,由图象面积,可得拉力做功为:
WF=
(6+8)×2+8×0.5=18J
根据功能关系可知电阻R上产生的焦耳热为:
Q=WF-
=18-16=2J
故拉力F作用过程中,电阻R上产生的焦耳热为
Q=1.5J.
答:(1)拉力F作用过程中,通过电阻R上电量是1.25c;
(2)导体杆运动过程中的最大速度是8m/s;
(3)拉力F作用过程中,电阻R上产生的焦耳热是1.5J.
q=
| . |
| I |
| . |
| I |
| E |
| R+r |
| . |
| E |
| △Φ |
| △t |
q=
| △Φ |
| R+r |
| BS |
| R+r |
(2)导体杆先做加速运动,后匀速运动,撤去拉力后减速运动.设最大速度为vm
撤去F后金属棒滑行过程中动能转化为电能
∵
| QR |
| Qr |
| 3 |
| 1 |
由能量守恒定律,得
| 1 |
| 2 |
| mv | 2m |
∴vm=8m/s.
故导体杆运动过程中的最大速度为8m/s.
(2)匀速运动时最大拉力与安培力平衡
再分析匀速运动阶段,最大拉力为:
Fm=BIml=
| B2l2 |
| R+r |
拉力F作用过程中,由图象面积,可得拉力做功为:
WF=
| 1 |
| 2 |
根据功能关系可知电阻R上产生的焦耳热为:
Q=WF-
| 1 |
| 2 |
| mv | 2m |
故拉力F作用过程中,电阻R上产生的焦耳热为
| 3 |
| 4 |
答:(1)拉力F作用过程中,通过电阻R上电量是1.25c;
(2)导体杆运动过程中的最大速度是8m/s;
(3)拉力F作用过程中,电阻R上产生的焦耳热是1.5J.

练习册系列答案
相关题目

 (2010?泰州模拟)如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道相距l=1m,两轨道之间用R=3Ω的电阻连接,一质量m=0.5kg、电阻r=1Ω的导体杆与两轨道垂直,静止放在轨道上,轨道的电阻可忽略不计.整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上,现用水平拉力沿轨道方向拉导体杆,拉力F与导体杆运动的位移s间的关系如图(乙)所示,当拉力达到最大时,导体杆开始做匀速运动,当位移s=2.5m时撤去拉力,导体杆又滑行了一段距离s'后停下,在滑行s'的过程中电阻R上产生的焦耳热为12J.求:
(2010?泰州模拟)如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道相距l=1m,两轨道之间用R=3Ω的电阻连接,一质量m=0.5kg、电阻r=1Ω的导体杆与两轨道垂直,静止放在轨道上,轨道的电阻可忽略不计.整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上,现用水平拉力沿轨道方向拉导体杆,拉力F与导体杆运动的位移s间的关系如图(乙)所示,当拉力达到最大时,导体杆开始做匀速运动,当位移s=2.5m时撤去拉力,导体杆又滑行了一段距离s'后停下,在滑行s'的过程中电阻R上产生的焦耳热为12J.求:
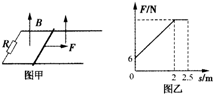 如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道相距l=1m,两轨道之间用R=2Ω的电阻连接,一质量m=0.5kg的导体杆与两轨道垂直,静止放在轨道上,杆及轨道的电阻均可忽略不计,整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上,现用水平拉力沿轨道方向拉导体杆,拉力F与导体杆运动的位移s间的关系如图(乙)所示,当拉力达到最大时,导体杆开始做匀速运动,当位移s=2.5m时撤去拉力,导体杆又滑行了s′=2m停下,求:
如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道相距l=1m,两轨道之间用R=2Ω的电阻连接,一质量m=0.5kg的导体杆与两轨道垂直,静止放在轨道上,杆及轨道的电阻均可忽略不计,整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上,现用水平拉力沿轨道方向拉导体杆,拉力F与导体杆运动的位移s间的关系如图(乙)所示,当拉力达到最大时,导体杆开始做匀速运动,当位移s=2.5m时撤去拉力,导体杆又滑行了s′=2m停下,求: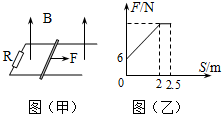 如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道相距L=1m,两轨道之间用R=3Ω的电阻连接,一质量m=0.5kg的导体杆与两轨道垂直,静止放在轨道上,轨道的电阻可忽略不计.整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上,现用水平拉力沿轨道方向拉导体杆,拉力F与导体杆运动的位移s间的关系如图(乙)所示,当拉力达到最大时,导体杆开始做匀速运动,当位移s=2.5m时撤去拉力,导体杆又滑行了一段距离s′后停止.已知在拉力F作用过程中,通过电阻R上电量q为1.25C.在滑行s′的过程中电阻R上产生的焦耳热为12J.求:
如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道相距L=1m,两轨道之间用R=3Ω的电阻连接,一质量m=0.5kg的导体杆与两轨道垂直,静止放在轨道上,轨道的电阻可忽略不计.整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上,现用水平拉力沿轨道方向拉导体杆,拉力F与导体杆运动的位移s间的关系如图(乙)所示,当拉力达到最大时,导体杆开始做匀速运动,当位移s=2.5m时撤去拉力,导体杆又滑行了一段距离s′后停止.已知在拉力F作用过程中,通过电阻R上电量q为1.25C.在滑行s′的过程中电阻R上产生的焦耳热为12J.求: