题目内容
小船从A码头出发,沿垂直于河岸的方向渡河,若小河宽为d,小船渡河速度v船恒定,河水中各点水流速大小与各点到较近河岸边的距离成正比,v水=kx,x是各点到近岸的距离(x≤d/2,k为常量),要使小船能够到达距A正对岸为s的B码头.则下列说法中正确的是( )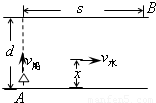
A.小船渡河的速度
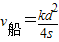
B.小船渡河的速度
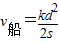
C.小船渡河的时间为
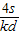
D.小船渡河的时间为
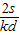
【答案】分析:将小船的运动分解为垂直于河岸方向和沿河岸方向,在垂直于河岸方向上,速度不变,位移随时间均匀增大,则水流速度随时间先均匀增大后均匀减小,分运动与合运动具有等时性,根据沿河岸方向的运动求出运行的时间,再根据t=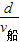 求出小船渡河的速度.
求出小船渡河的速度.
解答:解:小船在沿河岸方向的速度随时间先均匀增大后均匀减小,前 内和后
内和后 内的平均速度为
内的平均速度为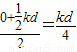 ,则渡河的时间t=
,则渡河的时间t=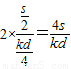 .渡河速度
.渡河速度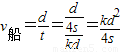 .故A、C正确,B、D错误.
.故A、C正确,B、D错误.
故选AC.
点评:解决本题的关键知道在垂直于河岸方向上做匀速直线运动,位移随时间均匀增大,根据河水中各点水流速大小与各点到较近河岸边的距离成正比,则水流速度随时间先均匀增大后均匀减小,从而根据匀变速直线运动求出平均速度.
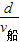 求出小船渡河的速度.
求出小船渡河的速度.解答:解:小船在沿河岸方向的速度随时间先均匀增大后均匀减小,前
 内和后
内和后 内的平均速度为
内的平均速度为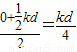 ,则渡河的时间t=
,则渡河的时间t=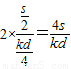 .渡河速度
.渡河速度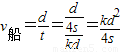 .故A、C正确,B、D错误.
.故A、C正确,B、D错误.故选AC.
点评:解决本题的关键知道在垂直于河岸方向上做匀速直线运动,位移随时间均匀增大,根据河水中各点水流速大小与各点到较近河岸边的距离成正比,则水流速度随时间先均匀增大后均匀减小,从而根据匀变速直线运动求出平均速度.

练习册系列答案
相关题目
 小船从A码头出发,沿垂直于河岸的方向渡河,若河宽为d,渡河速度v船恒定,河水的流速与到河岸的距离成正比,即v水=kx (x≤
小船从A码头出发,沿垂直于河岸的方向渡河,若河宽为d,渡河速度v船恒定,河水的流速与到河岸的距离成正比,即v水=kx (x≤| d |
| 2 |
A、v船应为
| ||
B、v船应为
| ||
C、渡河时间为
| ||
D、渡河时间为
|
 (2009?上海模拟)如图所示,小船从A码头出发,沿垂直于河岸的方向渡河,若河宽为d,渡河速度v船恒定,河水的流速与到河岸的距离x成正比,即v水=kx(x≤d/2,k为常量),要使小船能够到达距A正对岸距离为s远的B码头,则( )
(2009?上海模拟)如图所示,小船从A码头出发,沿垂直于河岸的方向渡河,若河宽为d,渡河速度v船恒定,河水的流速与到河岸的距离x成正比,即v水=kx(x≤d/2,k为常量),要使小船能够到达距A正对岸距离为s远的B码头,则( ) 小船从A码头出发,沿垂直于河岸的方向渡河,若小河宽为d,小船渡河速度v船恒定,河水中各点水流速度大小与各点到较近河岸边的距离成正比,v水=kx,x是各点到近岸的距离(x≤
小船从A码头出发,沿垂直于河岸的方向渡河,若小河宽为d,小船渡河速度v船恒定,河水中各点水流速度大小与各点到较近河岸边的距离成正比,v水=kx,x是各点到近岸的距离(x≤ 小船从A码头出发,沿垂直于河岸的方向渡河,若小河宽为d,小船渡河速度v船恒定,河水中各点水流速大小与各点到较近河岸边的距离成正比,v水=kx,x是各点到近岸的距离(x≤d/2,k为常量),要使小船能够到达距A正对岸为s的B码头.则下列说法中正确的是( )
小船从A码头出发,沿垂直于河岸的方向渡河,若小河宽为d,小船渡河速度v船恒定,河水中各点水流速大小与各点到较近河岸边的距离成正比,v水=kx,x是各点到近岸的距离(x≤d/2,k为常量),要使小船能够到达距A正对岸为s的B码头.则下列说法中正确的是( )