题目内容
12. 如图所示,在水平面上有两条光滑的长直平行金属导轨MN、PQ,电阻忽略不计,导轨间距离为L,磁感应强度为B的匀强磁场垂直于导轨所在平面.质量均为m的两根金属a、b放置在导轨上,a、b接入电路的电阻均为R.轻质弹簧的左端与b杆连接,右端固定.开始时a杆以初速度v0.向静止的b杆运动,当a杆向右的速度为v时,b杆向右的速度达到最大值vm,此过程中a杆产生的焦耳热为Q,两杆始终垂直于导轨并与导轨接触良好,则b杆达到最大速度时( )
如图所示,在水平面上有两条光滑的长直平行金属导轨MN、PQ,电阻忽略不计,导轨间距离为L,磁感应强度为B的匀强磁场垂直于导轨所在平面.质量均为m的两根金属a、b放置在导轨上,a、b接入电路的电阻均为R.轻质弹簧的左端与b杆连接,右端固定.开始时a杆以初速度v0.向静止的b杆运动,当a杆向右的速度为v时,b杆向右的速度达到最大值vm,此过程中a杆产生的焦耳热为Q,两杆始终垂直于导轨并与导轨接触良好,则b杆达到最大速度时( )| A. | b杆受到弹簧的弹力为$\frac{{B}^{2}{L}^{2}(v-{v}_{m})}{2R}$ | |
| B. | a杆受到的安培力为$\frac{{B}^{2}{L}^{2}(v-{v}_{m})}{R}$ | |
| C. | a、b杆与弹簧组成的系统机械能减少量为Q | |
| D. | 弹簧具有的弹性势能为$\frac{1}{2}$mv02-$\frac{1}{2}$mv2-$\frac{1}{2}$mvm2-2Q |
分析 b杆达到最大速度时,弹簧的弹力等于安培力,根据安培力大小公式与闭合电路欧姆定律及法拉第电磁感应定律,可得到弹簧的弹力;两棒安培力关系求出a杆受到的安培力.选取系统为研究对象,确定从开始到b杆最大速度作为过程,由能量守恒来确定弹簧的弹性势能.
解答 解:A、b杆达到最大速度时,弹簧的弹力等于安培力,由闭合电路欧姆定律可得 I=$\frac{E}{2R}$=$\frac{BL(v-{v}_{m})}{2R}$,b棒受到的安培力大小F=BIL=$\frac{{B}^{2}{L}^{2}(v-{v}_{m})}{2R}$,则弹簧的弹力为F=$\frac{{B}^{2}{L}^{2}(v-{v}_{m})}{2R}$,故A正确
B、a、b两棒串联,电流相等,长度相等,所受的安培力大小相等,所以a杆受到的安培力为$\frac{{B}^{2}{L}^{2}(v-{v}_{m})}{2R}$,故B错误;
C、根据能量守恒定律可知,、b杆与弹簧组成的系统机械能减少量为2Q.故C错误.
D、选两杆和弹簧组成系统为研究对象,从a棒开始运动到b棒达到最大速度,由能量守恒知,弹簧具有的弹性势能为$\frac{1}{2}$mv02-$\frac{1}{2}$mv2-$\frac{1}{2}$mvm2-2Q.故D正确;
故选:AD.
点评 由于两杆同时同向运动,切割的速度为相对速度,即两棒速度之差,同时考查闭合电路欧姆定律、法拉第电磁感应定律、动能定理及安培力大小公式,并注意安培力做功与产生焦耳热的关系,及弹力做功与弹簧的弹性势能的关系.

练习册系列答案
相关题目
7.在物理学中,原子,原子核及其更深层次的粒子统称为微观粒子,以下关于微观粒子的相关论述正确的是( )
| A. | 由大到小的关系为:分子→原子→原子核→质子→夸克 | |
| B. | 纳米科学技术的研究对象是比原子更小的微粒 | |
| C. | 物质的不同物态表现出不同的性质是由分子的排列决定的,与分子力无关 | |
| D. | 原子核几乎占据了原子的全部空间,电子绕着原子核高速旋转 |
3. 目前智能手机普遍采用了电容触摸屏.电容触摸屏是利用人体的电流感应进行工作的,它是一块四层复合玻璃屏,玻璃屏的内表面和夹层各涂一层ITO(纳米铟锡金属氧化物),夹层ITO涂层作工作面,四个角引出四个电极,当用户触摸电容触摸屏时,用户手指和工作面形成一个电容器,因为工作面上接有高频信号,电流通过这个电容器分别从屏的四个角上的电极中流出,且理论上流经四个电极的电流与手指头到四角的距离成比例,控制器通过对四个电流比例的精密计算来确定位置.对于电容触摸屏,下列说法正确的是( )
目前智能手机普遍采用了电容触摸屏.电容触摸屏是利用人体的电流感应进行工作的,它是一块四层复合玻璃屏,玻璃屏的内表面和夹层各涂一层ITO(纳米铟锡金属氧化物),夹层ITO涂层作工作面,四个角引出四个电极,当用户触摸电容触摸屏时,用户手指和工作面形成一个电容器,因为工作面上接有高频信号,电流通过这个电容器分别从屏的四个角上的电极中流出,且理论上流经四个电极的电流与手指头到四角的距离成比例,控制器通过对四个电流比例的精密计算来确定位置.对于电容触摸屏,下列说法正确的是( )
 目前智能手机普遍采用了电容触摸屏.电容触摸屏是利用人体的电流感应进行工作的,它是一块四层复合玻璃屏,玻璃屏的内表面和夹层各涂一层ITO(纳米铟锡金属氧化物),夹层ITO涂层作工作面,四个角引出四个电极,当用户触摸电容触摸屏时,用户手指和工作面形成一个电容器,因为工作面上接有高频信号,电流通过这个电容器分别从屏的四个角上的电极中流出,且理论上流经四个电极的电流与手指头到四角的距离成比例,控制器通过对四个电流比例的精密计算来确定位置.对于电容触摸屏,下列说法正确的是( )
目前智能手机普遍采用了电容触摸屏.电容触摸屏是利用人体的电流感应进行工作的,它是一块四层复合玻璃屏,玻璃屏的内表面和夹层各涂一层ITO(纳米铟锡金属氧化物),夹层ITO涂层作工作面,四个角引出四个电极,当用户触摸电容触摸屏时,用户手指和工作面形成一个电容器,因为工作面上接有高频信号,电流通过这个电容器分别从屏的四个角上的电极中流出,且理论上流经四个电极的电流与手指头到四角的距离成比例,控制器通过对四个电流比例的精密计算来确定位置.对于电容触摸屏,下列说法正确的是( )| A. | 电容触摸屏只需要触摸,不需要压力即能产生位置信号 | |
| B. | 使用绝缘笔,在电容屏上也能进行触控操作 | |
| C. | 手指压力变大时,由于手指与屏的夹层工作面距离变小,电容变小 | |
| D. | 手指与屏的接触面积变大时,电容变小 |
20. 如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=45°.则( )
如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=45°.则( )
 如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=45°.则( )
如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=45°.则( )| A. | 当风速v=3m/s时,F的大小恰好等于球的重力 | |
| B. | 当风速v=6m/s时,θ=90° | |
| C. | 水平风力F越大,球平衡时,细线所受拉力越小 | |
| D. | 换用半径相等,但质量较大的球,则当θ=45°时,v大于3m/s |
4.如图所示,一理想变压器原线圈接入一交流电源,副线圈电路中R1、R2、R3和R4均为固定电阻.开关S是闭合的,V1、V2和V3为理想电压表,读数分别为U1、U2和U3;A1、A2和A3为理想电流表,读数分别为I1、I2和I3.U1数值不变,现断开S,下列推断中正确的是( )
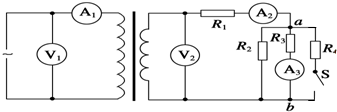

| A. | U2变小、I3变小 | B. | U2不变、I3变小 | C. | I1变小、I2变小 | D. | I1变小、I2变大 |


 如图大环半径是小金属环的2倍.穿过大环的磁场变化率为$\frac{△B}{△t}$时,大环中的感应电动势为ε.穿过小环中的磁场变化率也为$\frac{△B}{△t}$时,小环中感应电动势为$\frac{ε}{4}$.
如图大环半径是小金属环的2倍.穿过大环的磁场变化率为$\frac{△B}{△t}$时,大环中的感应电动势为ε.穿过小环中的磁场变化率也为$\frac{△B}{△t}$时,小环中感应电动势为$\frac{ε}{4}$.