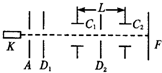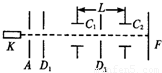题目内容
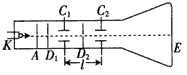
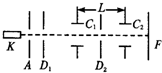利用双电容法可测量电子荷质比．装置如图所示，在真空管中由阴极K发射出电子，其初速度为零，此电子被阴极K与阳极A间电场加速度穿过屏障D1上的小孔，然后按顺序穿过电容器C1、屏D2和C2而射到荧光屏F上，阳极与阴极间的电压为U，分别在电容器C1、C2上加有频率为f的完全相同的交流电压，C1、C2之间的距离为L，选择频率为f，使电子束在荧光屏上不发生偏转．试根据以上数据求出电子的荷质比．分析：要使电子通过两电容器不发生偏转，电子通过两电容器C1与C2时，其电场恰好相反，再根据动能定理，即可求解．
解答：解：电子通过电容器时间极短，在此时间内可以认为加在电容器C1、C2上的交变电压值不变，
因而要使电子通过两电容器不发生偏转，电子通过两电容器C1与C2时，
其电场恰好相反：即满足
=
（n=1，2…）
电子加速时：Ue=
mv2
所以
=
答：根据以上数据求出电子的荷质比
=
．
因而要使电子通过两电容器不发生偏转，电子通过两电容器C1与C2时，
其电场恰好相反：即满足
| L |
| v |
| n |
| 2f |
电子加速时：Ue=
| 1 |
| 2 |
所以
| e |
| m |
| 2f2L2 |
| n2U |
答：根据以上数据求出电子的荷质比
| e |
| m |
| 2f2L2 |
| n2U |
点评：考查电子在电场中的运动情况来确定受力分析，并掌握动能定理的应用．注意电荷的荷质比也称比荷．
练习册系列答案
全能测控期末小状元系列答案
相关题目
上的小孔，然后依次穿过电容
、屏障
上的小孔和第二个电容器
而射到荧光屏F上．阳极A与阴极K之间电势差为U，
、
上加有频率为f的同一交流电压，
，则电子的荷质比是多少？
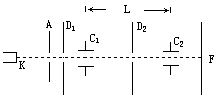
的最精确的方法之一是双电容法。如图所示，在真空管中由阴极K发射的电子，其初速度可忽略不计，此电子被阳极A的电场加速后穿过屏障D1上的小孔，然后依次穿过平行板电容器C1、屏障D2和第二个平行板电容器C2而射到荧光屏E上，阳极A与阴极K间的电势差为U。在电容器C1、C2之间加有频率为f的同步正弦交变电压，选择频率f使电子束在荧光屏上的亮点不发生偏转，且两电容器间的距离为l。试根据以上数据求出电子比荷。
