题目内容
 如图所示,BCD是光滑绝缘的、竖直固定的半径r=2.0m的圆轨道的一部分,CD为竖直直径,仅在BC间有方向竖直向下、高度足够高的匀强电场E,∠BOC=θ=53°.当一质量m=0.5kg的带电小球(可看成质点)P从距水平面AB高为h的地方以v0=7.2m/s的初速度水平抛出恰能无碰撞的从B点进入圆轨道,并从D点离开圆轨道,取g=10m/s2.已知:sin53°=0.8,cos53°=0.6.
如图所示,BCD是光滑绝缘的、竖直固定的半径r=2.0m的圆轨道的一部分,CD为竖直直径,仅在BC间有方向竖直向下、高度足够高的匀强电场E,∠BOC=θ=53°.当一质量m=0.5kg的带电小球(可看成质点)P从距水平面AB高为h的地方以v0=7.2m/s的初速度水平抛出恰能无碰撞的从B点进入圆轨道,并从D点离开圆轨道,取g=10m/s2.已知:sin53°=0.8,cos53°=0.6.(1)试求:小球从B点进入电场时的速度大小vB;
(2)若小球沿BC轨道的运动是匀速圆周运动.试问:
①小球刚到达D点时,小球对轨道的压力?
②小球离开D点再经多长的时间到达水平面AB?
分析:明确“水平抛出恰能无碰撞的从B点进入圆轨道”和“小球沿BC轨道的运动是匀速圆周运动”这两个题眼隐含的意义,即带电小球在B点的速度与OB垂直,在电场中带电小球所受重力与电场力是一对平衡力,且带电小球带负电荷.带电小球在重力作用下,由P点到B点做平抛运动,小球沿BC轨道的运动是匀速圆周运动,由C到D做圆周运动,由D点进入匀强电场做匀速直线运动,最后从电场出来在重力的作用下做平抛运动落地水平面上.
解答:解:设带电小球所带电量为q,小球到达B点的速度为VB,小球刚到达D点时,小球的速度为vD,轨道对小球的压力为F,匀强电场的宽度为d,带电小球过D点进入有界电场的时间为t1;从D点经过电场后,平抛运动的时间为t2,小球离开D点到达水平面AB的时间为t.
(1)、带电小球水平抛出恰能无碰撞的从B点进入圆轨道,即带电小球在B点的速度与OB垂直,由平抛运动在B点的速度分解公式可得:
VB=
=
=12m/s…①
(2)、小球沿BC轨道的运动是匀速圆周运动,在B到C中重力和电场力是一对平衡力,B到C过程,无力做功.
以B到D为研究过程,弹力不做功,无摩擦力,
由动能定理得:-mg2r=
mvD2 -
mvB2…②
以带电小球在D点为研究对象,有牛顿第二定律得:
mg+F=
… ③
联立①②③解之得:F=11N
根据牛顿第三定律得:小球对轨道的压力为11N,方向竖直向上.
通过D点后,在有界电场的位移,有几何关系得:d=rsin53°…④
过D点在有界匀强电场的时间为t1=
…⑤
带电小球通过匀强电场后做平抛运动,平抛运动的高度有几何关系 得:
hDA=2r-(r-rcos53°)…⑥
根据平抛运动竖直方向上的位移公式:hDA=
gt22 …⑦
小球离开D点再到达水平面AB的总时间为:t=t1+t2…⑧
联立①②④⑤⑥⑦⑧解之得:t=1s
答:(1)小球从B点进入电场时的速度大小为12m/s.
(2)①小球刚到达D点时,小球对轨道的压力为11N,方向竖直向上
②小球离开D点再经1s到达水平面AB.
(1)、带电小球水平抛出恰能无碰撞的从B点进入圆轨道,即带电小球在B点的速度与OB垂直,由平抛运动在B点的速度分解公式可得:
VB=
| v0 |
| cos530 |
| 7.2m/s |
| 0.6 |
(2)、小球沿BC轨道的运动是匀速圆周运动,在B到C中重力和电场力是一对平衡力,B到C过程,无力做功.
以B到D为研究过程,弹力不做功,无摩擦力,
由动能定理得:-mg2r=
| 1 |
| 2 |
| 1 |
| 2 |
以带电小球在D点为研究对象,有牛顿第二定律得:
mg+F=
| ||
| r |
联立①②③解之得:F=11N
根据牛顿第三定律得:小球对轨道的压力为11N,方向竖直向上.
通过D点后,在有界电场的位移,有几何关系得:d=rsin53°…④
过D点在有界匀强电场的时间为t1=
| d |
| vD |
带电小球通过匀强电场后做平抛运动,平抛运动的高度有几何关系 得:
hDA=2r-(r-rcos53°)…⑥
根据平抛运动竖直方向上的位移公式:hDA=
| 1 |
| 2 |
小球离开D点再到达水平面AB的总时间为:t=t1+t2…⑧
联立①②④⑤⑥⑦⑧解之得:t=1s
答:(1)小球从B点进入电场时的速度大小为12m/s.
(2)①小球刚到达D点时,小球对轨道的压力为11N,方向竖直向上
②小球离开D点再经1s到达水平面AB.
点评:抓住“水平抛出恰能无碰撞的从B点进入圆轨道”和“小球沿BC轨道的运动是匀速圆周运动”这两个题眼是解题的关键,分析带电小球的受力和运动情况是首要前提,明确运动过程中遵循的规律是突破点.

练习册系列答案
相关题目
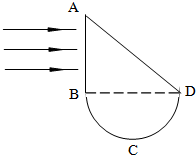 如图所示,ABCD为同种材料构成的柱形透明体的横截面,其中ABD部分为等腰直角三角形,BCD部分为半圆形,一束单色平行光从真空射向AB或AD面,材料折射率n=1.6,下列说法正确的是( )
如图所示,ABCD为同种材料构成的柱形透明体的横截面,其中ABD部分为等腰直角三角形,BCD部分为半圆形,一束单色平行光从真空射向AB或AD面,材料折射率n=1.6,下列说法正确的是( )| A、从AB面中点射入的光线一定从圆弧的中点射出 | B、从AB面射入的所有光线经一次反射和折射后都从BCD面射出 | C、从AB面中间附近射入的所有光线经一次反射和折射后都从BCD面射出 | D、若光线只从AD面垂直射入,则一定没有光线从BCD面射出 |
 如图所示,玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束频率5.3×1014Hz的单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角a=60°.已知光在真空中的速度c=3×108m/s,玻璃的折射率n=1.5,求:
如图所示,玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束频率5.3×1014Hz的单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角a=60°.已知光在真空中的速度c=3×108m/s,玻璃的折射率n=1.5,求: (2013?商丘三模)如图所示,玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束单色细光束从AD面的a点入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°.已知光在玻璃中的折射率n=1.5.求:
(2013?商丘三模)如图所示,玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束单色细光束从AD面的a点入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°.已知光在玻璃中的折射率n=1.5.求: (2013?日照一模)如图所示,玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束频率为5.3×1014 Hz的单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°.已知光在真空中的速度c=3×108m/s,玻璃的折射率n=1.5,求:
(2013?日照一模)如图所示,玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束频率为5.3×1014 Hz的单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°.已知光在真空中的速度c=3×108m/s,玻璃的折射率n=1.5,求: