题目内容
如图所示,两平行光滑的金属导轨MN、PQ固定在水平面上,相距为L,处于竖直向下的磁场中,整个磁场由n个宽度皆为x的条形匀强磁场区域1、2…n组成,从左向右依次排列,磁感应强度的大小分别为B、2B、3B…nB,两导轨左端MP间接入电阻R,一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上,与导轨电接触良好,不计导轨和金属棒的电阻.(1)对导体棒ab施加水平向右的力,使其从图示位置开始运动并穿过n个磁场区,求导体棒穿越磁场区1的过程中通过电阻R的电量q;
(2)对导体棒ab施加水平向右的恒力F,让它从磁场区1左侧边界处开始运动,当向右运动距离
 时做匀速运动,求棒通过磁场区1所用的时间t;
时做匀速运动,求棒通过磁场区1所用的时间t;(3)对导体棒ab施加水平向右的拉力,让它从距离磁场区1左侧x=x的位置由静止开始做匀加速运动,当棒ab进入磁场区1时开始做匀速运动,此后在不同的磁场区施加不同的拉力,使棒ab保持做匀速运动穿过整个磁场区,求棒ab通过第i磁场区时的水平拉力Fi和棒ab在穿过整个磁场区过程中回路产生的电热Q.

【答案】分析:(1)根据法拉第电磁感应定律求出平均电流,带入公式Q=It即可求出电量.
(2)线框开始做加速度逐渐减小的加速运动,然后匀速运动,对于变加速过程根据数学知识可以求出时间.
(3)根据动能定理可以求出导体棒进入磁场时速度大小,在磁场中匀速运动因此安培力等于力F1,根据受力平衡可以求出力F1,在磁场中运动时,导体棒克服安培力做功,转化为回路中的电热,根据功能关系写出安培力做功表达式,然后依据数学知识求解.
解答:解:(1)电路中产生的感应电动势为:
通过电阻R的电量为:
导体棒通过I区过程:△Φ=BLx
解得:
故导体棒穿越磁场区1的过程中通过电阻R的电量: .
.
(2)设导体棒运动时速度为v,则产生的感应电流为:

导体棒受到的安培力与水平向右的恒力F平衡,则
BIL=F
解得:
设棒通过磁场去I在△t时间内速度的变化为△v,对应的位移为△x,则


则
解得:
故棒通过磁场区1所用的时间 .
.
(3)设进入I区时拉力为F1,速度v,则有:


解得: ,
,
进入i区的拉力: .
.
导体棒以后通过每区域都以速度v做匀速运动,由功能关系有:
Q=F1x+F2x+…+Fnx
解得:
故棒ab通过第i磁场区时的水平拉力的拉力: ,棒ab在穿过整个磁场区过程中回路产生的电热
,棒ab在穿过整个磁场区过程中回路产生的电热 .
.
点评:本题考查了电磁感应中力学与功能问题,物理过程比较简单,难点在于应用数学知识解答物理问题.
(2)线框开始做加速度逐渐减小的加速运动,然后匀速运动,对于变加速过程根据数学知识可以求出时间.
(3)根据动能定理可以求出导体棒进入磁场时速度大小,在磁场中匀速运动因此安培力等于力F1,根据受力平衡可以求出力F1,在磁场中运动时,导体棒克服安培力做功,转化为回路中的电热,根据功能关系写出安培力做功表达式,然后依据数学知识求解.
解答:解:(1)电路中产生的感应电动势为:

通过电阻R的电量为:

导体棒通过I区过程:△Φ=BLx
解得:

故导体棒穿越磁场区1的过程中通过电阻R的电量:
 .
.(2)设导体棒运动时速度为v,则产生的感应电流为:

导体棒受到的安培力与水平向右的恒力F平衡,则
BIL=F
解得:

设棒通过磁场去I在△t时间内速度的变化为△v,对应的位移为△x,则


则

解得:

故棒通过磁场区1所用的时间
 .
.(3)设进入I区时拉力为F1,速度v,则有:


解得:
 ,
,
进入i区的拉力:
 .
.导体棒以后通过每区域都以速度v做匀速运动,由功能关系有:
Q=F1x+F2x+…+Fnx
解得:

故棒ab通过第i磁场区时的水平拉力的拉力:
 ,棒ab在穿过整个磁场区过程中回路产生的电热
,棒ab在穿过整个磁场区过程中回路产生的电热 .
.点评:本题考查了电磁感应中力学与功能问题,物理过程比较简单,难点在于应用数学知识解答物理问题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图所示,两平行光滑导轨相距为L=20cm,金属棒MN的质量为m=10g,电阻R=8Ω,匀强磁场的磁感应强度B=0.8T,方向竖直向下,电源电动势E=10V,内阻r=1Ω,当开关S闭合时,MN恰好平衡.
如图所示,两平行光滑导轨相距为L=20cm,金属棒MN的质量为m=10g,电阻R=8Ω,匀强磁场的磁感应强度B=0.8T,方向竖直向下,电源电动势E=10V,内阻r=1Ω,当开关S闭合时,MN恰好平衡.

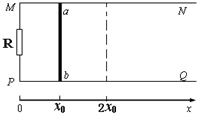 如图所示,两平行光滑金属导轨MN、PQ被固定在同一水平面内,间距为L,电阻不计.导轨的M、P两端用导线连接一定值电阻,阻值为R,在PM的右侧0到2x0区域里有方向竖直向下的磁场,其磁感应强度B随坐标x的变化规律为B=kx(k为正常数).一直导体棒ab长度为L,电阻为R,其两端放在导轨上且静止在x=x0处,现对导体棒持续施加一作用力F(图中未画出)使导体棒从静止开始做沿x正方向加速度为a的匀加速运动,求:(用L、k、R、x0、a表示):
如图所示,两平行光滑金属导轨MN、PQ被固定在同一水平面内,间距为L,电阻不计.导轨的M、P两端用导线连接一定值电阻,阻值为R,在PM的右侧0到2x0区域里有方向竖直向下的磁场,其磁感应强度B随坐标x的变化规律为B=kx(k为正常数).一直导体棒ab长度为L,电阻为R,其两端放在导轨上且静止在x=x0处,现对导体棒持续施加一作用力F(图中未画出)使导体棒从静止开始做沿x正方向加速度为a的匀加速运动,求:(用L、k、R、x0、a表示):