题目内容
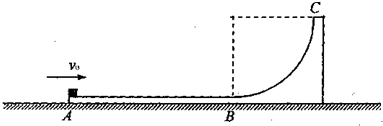
竖直平面内的轨道ABC由水平滑道AB与光滑的四分之一圆弧道BC平滑连接组成,轨道放在光滑的水平面上.一个质量为m=1kg的小物块(可视为质点)从轨道的A端以初速度v=8m/s冲上水平滑道AB,沿着轨道运动,由CB弧滑下后停在水平滑道AB的中点.已知轨道ABC的质量为M=3kg.求:(1)小物块和滑道相对静止时共同的速度;
(2)若小物块恰好不从C端离开滑道,圆弧滑道的半径R应是多大?
(3)若增大小物块的初速度,使得小物块冲出轨道后距离水平滑道AB的最大高度是2R,小物块的初速度v应多大.

【答案】分析:(1)物块冲上滑道AB后的运动过程中,系统水平方向不受外力,动量守恒,物块最终与滑道的速度相同,由动量守恒定律求最终速度;
(2)若小物块刚好到达D处,此时它与轨道有共同的速度,此速度与上题最终速度相等,根据整个过程功能关系列式求解.
(3)根据动量守恒和能量定恒列出等式求解.
解答:解:(1)小物块冲上轨道的初速度设为v,最终停在AB的中点,跟轨道有相同的速度,设为V1.在这个过程中由系统动量定恒有
mv=(M+m)v1①
可得v1=2m/s②
(2)小物块冲上轨道到最终停在AB的中点,设物块与轨道间滑动摩擦力为f,由能量定恒
 fL=
fL= m
m -
- (M+m)
(M+m) ③
③
若小物块恰好到达C端,此时它与轨道有共同的速度V1,在此过程中系统总的动能减少转化为内能和物块的势能
fL+mgR= m
m -
- (M+m)
(M+m) ④
④
由③、④解得,要使物块恰好不从C点离开滑道,圆弧半径应为
R=0.8m⑤
(3)设物块以初速度v′上轨道,可以在到的最大高度为2R,物块从C点离开轨道,其水平方向的速度总与轨道速度相等,达到最高点时,
物块水平跟轨道的速度相等(设为V2)
mv′=(m+M)v2 ⑥
 m
m =
= (m+M)
(m+M) +mg?2R+fL⑦
+mg?2R+fL⑦
由⑥、⑦可得 =9.25m/s
=9.25m/s
答:(1)小物块和滑道相对静止时共同的速度是2m/s;
(2)若小物块恰好不从C端离开滑道,圆弧滑道的半径R应是0.8m
(3)若增大小物块的初速度,使得小物块冲出轨道后距离水平滑道AB的最大高度是2R,小物块的初速度v应是9.25m/s
点评:能根据动量守恒条件判断系统动量守恒并能列式求解,能根据机械能守恒条件判断系统机械能守恒并列式求解是解决本题两问的关键.
(2)若小物块刚好到达D处,此时它与轨道有共同的速度,此速度与上题最终速度相等,根据整个过程功能关系列式求解.
(3)根据动量守恒和能量定恒列出等式求解.
解答:解:(1)小物块冲上轨道的初速度设为v,最终停在AB的中点,跟轨道有相同的速度,设为V1.在这个过程中由系统动量定恒有
mv=(M+m)v1①
可得v1=2m/s②
(2)小物块冲上轨道到最终停在AB的中点,设物块与轨道间滑动摩擦力为f,由能量定恒
 fL=
fL= m
m -
- (M+m)
(M+m) ③
③若小物块恰好到达C端,此时它与轨道有共同的速度V1,在此过程中系统总的动能减少转化为内能和物块的势能
fL+mgR=
 m
m -
- (M+m)
(M+m) ④
④由③、④解得,要使物块恰好不从C点离开滑道,圆弧半径应为
R=0.8m⑤
(3)设物块以初速度v′上轨道,可以在到的最大高度为2R,物块从C点离开轨道,其水平方向的速度总与轨道速度相等,达到最高点时,
物块水平跟轨道的速度相等(设为V2)
mv′=(m+M)v2 ⑥
 m
m =
= (m+M)
(m+M) +mg?2R+fL⑦
+mg?2R+fL⑦由⑥、⑦可得
 =9.25m/s
=9.25m/s答:(1)小物块和滑道相对静止时共同的速度是2m/s;
(2)若小物块恰好不从C端离开滑道,圆弧滑道的半径R应是0.8m
(3)若增大小物块的初速度,使得小物块冲出轨道后距离水平滑道AB的最大高度是2R,小物块的初速度v应是9.25m/s
点评:能根据动量守恒条件判断系统动量守恒并能列式求解,能根据机械能守恒条件判断系统机械能守恒并列式求解是解决本题两问的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
 (2012?黄埔区模拟)如图所示,一个固定在竖直平面内的轨道,有倾角为θ=37°的斜面AB和水平面BC以及另一个倾角仍为θ=37°的斜面DE三部分组成.已知水平面BC长为0.4m,D位置在C点的正下方,CD高为H=0.9m,E点与C点等高,P为斜面DE的中点;小球与接触面间的动摩擦因数均为μ=0.15,重力加速度g取10m/s2.现将此小球离BC水平面400h高处的斜面上静止释放,小球刚好能落到P点(sin37°=0.6,cos37°=0.8).
(2012?黄埔区模拟)如图所示,一个固定在竖直平面内的轨道,有倾角为θ=37°的斜面AB和水平面BC以及另一个倾角仍为θ=37°的斜面DE三部分组成.已知水平面BC长为0.4m,D位置在C点的正下方,CD高为H=0.9m,E点与C点等高,P为斜面DE的中点;小球与接触面间的动摩擦因数均为μ=0.15,重力加速度g取10m/s2.现将此小球离BC水平面400h高处的斜面上静止释放,小球刚好能落到P点(sin37°=0.6,cos37°=0.8).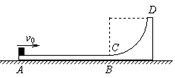 如图所示,竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成,AB恰与圆弧CD在C点相切,轨道固定在水平面上.一个质量为m的小物块(可视为质点)从轨道的A端以初动能E冲上水平轨道AB,沿着轨道运动,由DC弧滑下后停在水平轨道AB的中点.已知水平轨道AB长为L.求:
如图所示,竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成,AB恰与圆弧CD在C点相切,轨道固定在水平面上.一个质量为m的小物块(可视为质点)从轨道的A端以初动能E冲上水平轨道AB,沿着轨道运动,由DC弧滑下后停在水平轨道AB的中点.已知水平轨道AB长为L.求: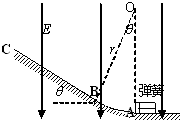 如图所示,ABC为固定在竖直平面内的轨道,AB段为光滑圆弧,对应的圆心角θ=37°,OA竖直,半径r=2.5m,BC为足够长的平直倾斜轨道,倾角θ=37°.已知斜轨BC与小物体间的动摩擦因数μ=0.25.各段轨道均平滑连接,轨道所在区域有E=4×103N/C、方向竖直向下的匀强电场.质量m=5×10-2kg、电荷量q=+1×10-4C的小物体(视为质点)被一个压紧的弹簧发射后,沿AB圆弧轨道向左上滑,在B点以速度v0=3m/s冲上斜轨.设小物体的电荷量保持不变.重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.(设弹簧每次均为弹性形变.)
如图所示,ABC为固定在竖直平面内的轨道,AB段为光滑圆弧,对应的圆心角θ=37°,OA竖直,半径r=2.5m,BC为足够长的平直倾斜轨道,倾角θ=37°.已知斜轨BC与小物体间的动摩擦因数μ=0.25.各段轨道均平滑连接,轨道所在区域有E=4×103N/C、方向竖直向下的匀强电场.质量m=5×10-2kg、电荷量q=+1×10-4C的小物体(视为质点)被一个压紧的弹簧发射后,沿AB圆弧轨道向左上滑,在B点以速度v0=3m/s冲上斜轨.设小物体的电荷量保持不变.重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.(设弹簧每次均为弹性形变.) (2011?绍兴二模)如图所示,一个固定在竖直平面内的轨道,有倾角为θ=30°的斜面AB、光滑的水平面BO及圆心在O点、半径
(2011?绍兴二模)如图所示,一个固定在竖直平面内的轨道,有倾角为θ=30°的斜面AB、光滑的水平面BO及圆心在O点、半径