题目内容
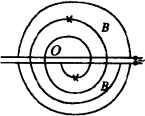
如图所示,粒子回旋加速器由两个D形盒组成,在D形盒的缝隙处加交变电压,整个装置处在匀强磁场中.从O点输入的带电粒子经过电场加速和磁偏转的反复运动,最终可以从边缘由导出装置导出.已知交流电压的频率等于粒子在磁场中回旋的频率.试讨论:粒子射出时速度vm的大小由哪些因素决定.
解析:
|
答案:只要粒子从D形盒边缘被导出,那么,它最后半周应满足:qvmB=mvm2/R, 即:vm=qBR/m. 可见要使粒子射出时的速度vm大,就要使磁场的磁感应强度B以及D形盒的半径R增大,而与加速电压U的大小无关(U≠0). 粒子经电压加速后进入磁场做匀速圆周运动,回旋半周后又进入电场,由于交变电压的周期等于粒子回旋的周期(与粒子速率大小无关),所以,进入电场后继续被加速,再进入磁场做半径更大的匀速圆周运动…如此反复,直到从边缘被导出,以上就是粒子被回旋加速的过程. 由于加速的时间很短,所以,一方面加速电压可视为定值设为U;另一方面在缝隙加速过程中,洛伦兹力引起的粒子的偏转极小,可略去不计. 粒子射出时的最大速度vm的大小由哪些因素决定呢? 设被加速的粒子的电量为q,质量为m,加速电压为U,磁场的磁感应强度为B,D形盒的半径为R. 下面给出两种不同的观点,试判断哪个是正确的? 观点1:使粒子获得动能的是电场.设共加速n次,则由动能定理有 由上式可知,为了使粒子射出时的速度vm增大,只需增大加速电压而与磁场的磁感应强度大小及D形盒半径的大小无关. 观点2:只要粒子从D形盒边缘被导出,那么,它最后半周应满足:qvmB=mvM2/R,即vm=qBR/m. 可见要使粒子射出时的速度vm大,就要使磁场的磁感应强度B以及D形盒的半径R增大,而与加速电压U的大小无关(U≠0). 以上两种观点中哪个是对的呢? 从讨论的一般原则看,判断两个量之间的函数关系,其他量应是不变的或相同的,这样看,观点2是正确的. 观点1的错误就在于没有注意到公式中的加速次数n恰是电压U的函数,因此电压越高,加速的次数就越少.设想如果电压足够大,则粒子有可能旋转半周就被导出了. 我们知道,理论上讲,仅靠电场加速也可以使粒子获得较大的速度,例如直线加速器就是靠电场加速的.但电场加速的困难在于加速电压不能提高到足够大,要受绝缘的限制,而粒子回旋加速器正是采取低电压和多次加速积累,使粒子获得足够大的能量,它是粒子交替受电场力和洛伦兹力作用的实例. |

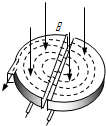 回旋加速器是用来加速带电粒子的装置,如图所示.它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核(
回旋加速器是用来加速带电粒子的装置,如图所示.它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核(3 1 |
4 2 |
| A、加速氚核的交流电源的周期较大 |
| B、加速α粒子的交流电源的周期较大 |
| C、加速氚核获得的最大动能也较小 |
| D、加速α粒子获得的最大动能较大 |
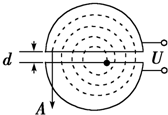 如图所示,回旋加速器D形盒的半径为R,所加磁场的磁感应强度为B,用来加速质量为m、电荷量为q的质子,质子从下半盒的质子源由静止出发,加速到最大动能E后由A孔射出,则下列说法正确的是( )
如图所示,回旋加速器D形盒的半径为R,所加磁场的磁感应强度为B,用来加速质量为m、电荷量为q的质子,质子从下半盒的质子源由静止出发,加速到最大动能E后由A孔射出,则下列说法正确的是( )| A、回旋加速器不能无限加速粒子 | ||||
| B、质子在加速器中运行时间与交变电压U大小无关 | ||||
C、回旋加速器所加交变电压的频率为
| ||||
D、下半盒内部质子的轨道半径之比(由内到外)为1:
|
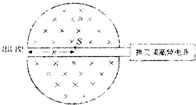 如图所示为回旋加速器的原理示意图,其核心部分是两个靠得非常近的D形盒,两盒分别和一高频交流电源的两极相连,交流高频电源的电压为U,匀强磁场分布在两D形盒内且垂直D形盒所在平面,磁感应强度为B,在D形盒中央S点处放有粒子源.粒子源放出质量为m、带电量为q的粒子(设粒子的初速度为零)被回旋加速器加速,设D形盒的最大半径为R,则( )
如图所示为回旋加速器的原理示意图,其核心部分是两个靠得非常近的D形盒,两盒分别和一高频交流电源的两极相连,交流高频电源的电压为U,匀强磁场分布在两D形盒内且垂直D形盒所在平面,磁感应强度为B,在D形盒中央S点处放有粒子源.粒子源放出质量为m、带电量为q的粒子(设粒子的初速度为零)被回旋加速器加速,设D形盒的最大半径为R,则( ) 回旋加速器是用来加速带电粒子的装置,如图所示.如果用同一回旋加速器分别加速氚核(
回旋加速器是用来加速带电粒子的装置,如图所示.如果用同一回旋加速器分别加速氚核(