题目内容
一根轻弹簧上端固定在O点，下端栓一个钢球P，球处于静止状态．现对球施加-个向右的外力F，使球缓慢偏移依次至A点和B点，如图所示．在移动中的每一个时刻，都可以认为钢球处于平衡状态．若外力F方向始终水平，移动中弹簧与竖直方向的夹角θ＜90°且弹簧的伸长量不超过弹性限度，则关于A、B两点的竖直高度，下列说法中正确的是（ ）分析：以小球为研究对象，分析受力情况，由平衡条件和胡克定律得到弹簧的伸长量与cosθ的关系式，再根据几何关系求解．
解答：解：对小球进行研究，分析受力情况：重力mg、水平外力F和弹簧的弹力f．由平衡条件得
f=
又由胡克定律得f=kx
则有 kx=
得 x=
所以弹簧在竖直方向的高度h=（L+x）cosθ=Lcosθ+
所以A、B两点距O点的竖直高度关系是hB＜hA
所以A点比B点低．
故选B．
f=| mg |
| cosθ |
又由胡克定律得f=kx
则有 kx=
| mg |
| cosθ |
得 x=
| mg |
| kcosθ |
所以弹簧在竖直方向的高度h=（L+x）cosθ=Lcosθ+
| mg |
| k |
所以A、B两点距O点的竖直高度关系是hB＜hA
所以A点比B点低．
故选B．
点评：本题是平衡条件与胡克定律的综合应用，分析受力情况是解题的关键，
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
（2011?徐州模拟）如图所示，一根轻弹簧上端固定在O点，下端拴一个钢球P，球处于静止状态．现对球施加一个方向向右的外力F，使球缓慢偏移，在移动中的每一个时刻，都可以认为钢球处于平衡状态．若外力F的方向始终水平，移动中弹簧与竖直方向的夹角θ＜90°，且弹簧的伸长量不超过其弹性限度，则下图给出的弹簧伸长量x与cosθ的函数关系图象中，最接近的是（ ）
如图所示，一根轻弹簧上端固定在天花板上，下端连在物体B上，现把楔形物体A与B叠放在一起置于水平面上保持静止，并使弹簧刚好处于竖直状态．有关物体A、B的受力分析中正确的是（ ）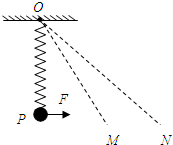
（2013?常德模拟）如图所示，一根轻弹簧上端固定在O点，下端拴一个小球P，开始时，小球处于静止状态．现对小球施加一个水平向右的外力F，使小球向右缓慢偏移，依次经过A点和B点，已知A、B两点分别在直线OM和ON上，但图中未标出具体位置，弹簧的伸长量始终处于弹性限度内，下列说法中正确的是（ ）
