题目内容
一轻绳两端各系一小物体A和B，且mA＞mB，跨放在一个光滑的半圆柱体上，半圆柱体的半径为R，A、B刚好贴在圆柱体的截面水平直径两端，如图所示．让两球由静止释放，当B到达圆柱体的最高点时，刚好脱离圆柱体，则：（1）B到最高点的速度 ．（2）mA：mB为 ．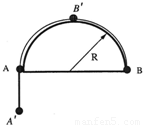
【答案】分析：（1）当B到达圆柱体的最高点时，刚好脱离圆柱体时，由重力提供向心力，根据牛顿第二定律列式求解B到最高点的速度．
（2）mA和mB组成的系统，只有重力做功，系统机械能守恒，根据系统机械能守恒定律列式求出mA：mB．
解答：解：（1）当B到达圆柱体的最高点时，刚好脱离圆柱体时，由重力提供向心力，根据牛顿第二定律得
mBg=mB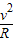
则得 v=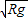
（2）根据系统的机械能守恒得：
mBgR+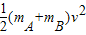
=mAg?
联立以上两式得：mA：mB=3：（π-1）
故答案为：（1）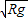
；（2）3：（π-1）
点评：解决本题的关键知道单个物体由于有拉力做功，机械能不守恒，对于系统而言，只有重力做功，机械能守恒．
（2）mA和mB组成的系统，只有重力做功，系统机械能守恒，根据系统机械能守恒定律列式求出mA：mB．
解答：解：（1）当B到达圆柱体的最高点时，刚好脱离圆柱体时，由重力提供向心力，根据牛顿第二定律得
mBg=mB
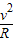
则得 v=
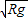
（2）根据系统的机械能守恒得：
mBgR+
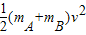=mAg?联立以上两式得：mA：mB=3：（π-1）
故答案为：（1）
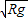；（2）3：（π-1）点评：解决本题的关键知道单个物体由于有拉力做功，机械能不守恒，对于系统而言，只有重力做功，机械能守恒．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
如图所示，一轻绳两端各系重物A和B，挂在汽车顶部的定滑轮上，绳的质量及滑轮摩擦均不计，mA＞mB，A静止在汽车底板上，轻绳呈竖直方向．当汽车在水平公路上匀速行驶时，A对汽车底板的压力为
一轻绳两端各系一小物体A和B，且mA＞mB，跨放在一个光滑的半圆柱体上，半圆柱体的半径为R，A、B刚好贴在圆柱体的截面水平直径两端，如图所示．让两球由静止释放，当B到达圆柱体的最高点时，刚好脱离圆柱体，则：（1）B到最高点的速度
