题目内容
 如图所示,粗糙弧形轨道和两个光滑半圆形轨道组成翘S形尾巴的轨道.已知两个半圆轨道的半径均为R,端点B、C、D、E在同一竖直线上,连接处C、D间有较小空隙,刚好能够让小球通过,C、D间的距离可忽略.粗糙弧形轨道最高点A与圆形轨道最低点B的高度为h.从A点由静止释放一个可看做质点的小球,球过B点无能量损失,小球沿轨道运动后从E点水平飞出,落到水平地面上,落点F到B点的水平距离为s.已知小球的质量为m,不计空气阻力,求:
如图所示,粗糙弧形轨道和两个光滑半圆形轨道组成翘S形尾巴的轨道.已知两个半圆轨道的半径均为R,端点B、C、D、E在同一竖直线上,连接处C、D间有较小空隙,刚好能够让小球通过,C、D间的距离可忽略.粗糙弧形轨道最高点A与圆形轨道最低点B的高度为h.从A点由静止释放一个可看做质点的小球,球过B点无能量损失,小球沿轨道运动后从E点水平飞出,落到水平地面上,落点F到B点的水平距离为s.已知小球的质量为m,不计空气阻力,求:(1)小球从E点水平飞出时的速度大小.
(2)小球运动到E点时对轨道的压力大小.
(3)小球沿轨道运动过程中克服摩擦力所做的功.
【答案】分析:(1)小球从E点飞出做平抛运动,根据高度求出运动的时间,再根据水平位移和时间求出平抛运动的初速度.
(2)在E点,沿半径方向上的合力提供向心力,根据牛顿第二定律求出轨道对球的弹力,从而根据牛顿第三定律求出小球对轨道的压力.
(3)根据动能定理求出小球沿轨道运动过程中克服摩擦力所做的功.
解答:解:(1)小球从E点飞出后做平抛运动,设在E点的速度大小为v,则:
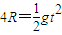
s=vt
解得: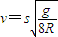 .
.
(2)设小球在E点对轨道的压力为F,对小球则:
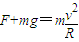
解得:F=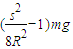
根据牛顿第三定律得: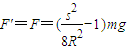 .
.
(3)设小球A到E点克服摩擦力做功为W,则由动能定理得:
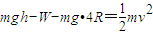
解得:W=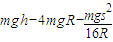 .
.
答:(1)小球从E点水平飞出时的速度大小为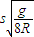 .
.
(2)小球运动到E点时对轨道的压力大小为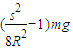 .
.
(3)小球沿轨道运动过程中克服摩擦力所做的功为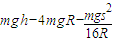 .
.
点评:解决本题的关键理清运动的过程,综合运用牛顿定律和动能定理进行解题.
(2)在E点,沿半径方向上的合力提供向心力,根据牛顿第二定律求出轨道对球的弹力,从而根据牛顿第三定律求出小球对轨道的压力.
(3)根据动能定理求出小球沿轨道运动过程中克服摩擦力所做的功.
解答:解:(1)小球从E点飞出后做平抛运动,设在E点的速度大小为v,则:
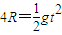
s=vt
解得:
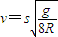 .
.(2)设小球在E点对轨道的压力为F,对小球则:
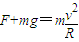
解得:F=
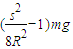
根据牛顿第三定律得:
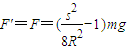 .
.(3)设小球A到E点克服摩擦力做功为W,则由动能定理得:
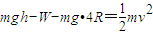
解得:W=
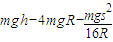 .
.答:(1)小球从E点水平飞出时的速度大小为
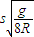 .
.(2)小球运动到E点时对轨道的压力大小为
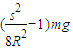 .
.(3)小球沿轨道运动过程中克服摩擦力所做的功为
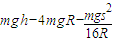 .
.点评:解决本题的关键理清运动的过程,综合运用牛顿定律和动能定理进行解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

