题目内容
8.汽车以36km/h的速度匀速行驶.(1)若汽车以0.6m/s2 的加速度加速,则10s后速度能达到多少?
(2)若汽车刹车以0.5m/s2的加速度减速,则10s后速度减为多少?
(3)若汽车刹车以2m/s2的加速度减速,则10s后位移是多少?
分析 (1)根据匀变速直线运动的速度时间公式求出10s后汽车的速度;
(2)判断出汽车减速所需时间,根据速度时间公式求得速度;
(3)判断出减速时间,根据位移时间公式求得位移
解答 解(1)加速时,加速度方向与速度方向相同,故a1=0.6m/s2,根据速度时间关系有,汽车10s末的速度v1=v0+a1t=10+0.6×10m/s=16m/s
(2)减速时,加速度方向与速度方向相反,故a2=-0.5m/s2,根据速度时间关系V=V0+a t 得:车停止所用时间为t=$\frac{10}{0.5}s=20s$ 10s<20s 车未停下.
汽车10s末的速度v2=v0+a2t=10+(-0.5)×10m/s=5m/s
(3)减速时,加速度方向与速度方向相反,故a3=-2m/s2,根据速度时间关系有:
车停止所用时间为t=$\frac{v}{a}$=$\frac{10}{2}s$=5s,10s>5s,车5s已停下.由v2-v02=2ax 得X=25m
答:(1)若汽车以0.6m/s2 的加速度加速,则10s后速度能达到16m/s
(2)若汽车刹车以0.5m/s2的加速度减速,则10s后速度减为5m/s
(3)若汽车刹车以2m/s2的加速度减速,则10s后位移是25m
点评 解决本题的关键掌握匀变速直线运动的速度时间公式v=v0+at,和位移时间公式,抓住减速过程减速到零所需时间,并能灵活运用

练习册系列答案
相关题目
18. 如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.则下列判断正确的是( )
如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.则下列判断正确的是( )
 如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.则下列判断正确的是( )
如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.则下列判断正确的是( )| A. | 四个点中c点处的电势最低,a 点电势最高 | |
| B. | b、d两点处的电场强度相同、电势相同 | |
| C. | b、d两点处的电场强度相同、电势不相同 | |
| D. | 将一试探电荷-q沿圆周由a点移至c点,-q的电势能增加 |
19.某同学“探究弹力与弹簧伸长量的关系”.步骤如下:
(1)弹簧自然悬挂,待弹簧静止时,长度记为L0;弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6.数据如下表.
由表可知所用刻度尺的最小分度为1mm.
(2)如图所示是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与Lx的差值(填“L0”或“Lx”).

(3)由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g.(结果保留两位有效数字,重力加速度g取9.8m/s2)
(1)弹簧自然悬挂,待弹簧静止时,长度记为L0;弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6.数据如下表.
| 代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
| 数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.40 | 35.35 | 37.40 | 39.30 |
(2)如图所示是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与Lx的差值(填“L0”或“Lx”).

(3)由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g.(结果保留两位有效数字,重力加速度g取9.8m/s2)
16.关于力的说法错误的是( )
| A. | 力可以改变物体的运动状态,也可以改变物体的形状 | |
| B. | 空中飞行的炮弹没有受到与前进方向相同的推力 | |
| C. | 几何形状规则的物体,其重心必然在物体的几何中心上 | |
| D. | 重心是物体总重力的等效作用点 |
18.有一物体做直线运动,其v-t图象如图所示,从图知,物体加速度和速度方向相同的时间间隔( )
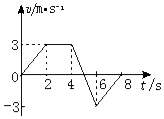

| A. | 0<t<2 s | B. | 4 s<t<5s | C. | 5s<t<6s | D. | 6s<t<8s |

 一物体(可视为质点)以一定的初速度冲上一倾角为θ的斜面,最后静止在斜面上,如图所示,已知物体在第1s内位移为6m,停止运动前的最后1s内位移为2m,求:
一物体(可视为质点)以一定的初速度冲上一倾角为θ的斜面,最后静止在斜面上,如图所示,已知物体在第1s内位移为6m,停止运动前的最后1s内位移为2m,求: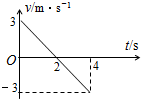 你可能到公园或游乐园蹦床.如图所示是一同学某次蹦床跳起后的v-t图象,结合你的体会和经历,回答下列问题:
你可能到公园或游乐园蹦床.如图所示是一同学某次蹦床跳起后的v-t图象,结合你的体会和经历,回答下列问题: