Question

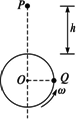
如图所示，小球Q在竖直平面内做匀速圆周运动，半径为r，当球Q运动到与O在同一水平线上时，有另一小球P在距圆周最高点为h处开始自由下落．要使两球在圆周最高点处相碰，Q球的角速度ω应满足什么条件？

Answer 1

答案：
解析：

解：自由落体的位移公式h＝gt2，可求得小球P自由下落运动至圆周最高点的时间为t1设小球Q做匀速圆周运动的周期为T，则有T＝ 　　由题意知，球Q由图示位置运动至圆周最高点所用时间为t2＝(n＋)T 　　式中n＝0，1，2，… 　　要使两球在圆周最高点相碰，需使t1＝t2　　④ 　　以上四式联立，解得球Q做匀速圆周运动的角速度为ω＝π(4n＋1) 　　式中n＝0，1，2，… 　　要使两球在圆周最高点处相碰，Q球的角速度ω应满足ω＝π(4n＋1)(n＝0，1，2，…)． 　　解析：小球Q在竖直平面内做匀速圆周运动具有重复性特点，要求小球P在距圆周最高点为h处开始自由下落至在圆周最高点处相碰，则在小球P下落时间内小球Q转过(n＋)圈，即小球P下落时间是小球Q匀速圆周运动的(n＋)倍．由此切入列方程即可求解． 　　方法归纳　注意此处空半格题目中两球相碰的条件为：两者在相同的时间内到达相同的空间位置．这一点是追及、相遇类问题的切入点．本题的关键是正确写出小球Q运动至最高点所需时间的通式．其中，由于匀速圆周运动具有重复性，故注意多解的产生．