题目内容
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1 m,导轨平面与水平面成θ=37°,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.2 kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25。
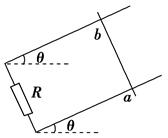
(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8 W,求该速度的大小;
(3)在上问中,若R=2 Ω,金属棒中的电流方向由a到b,求磁感应强度的大小与方向.(g取10 m/s2,sin37°=0.6,cos37°=0.8)
(1)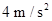 (2)10m/s
(3)0.4T 方向垂直于导轨平面向上
(2)10m/s
(3)0.4T 方向垂直于导轨平面向上
【解析】
试题分析:(1)金属棒开始下滑的初速度为零,根据牛顿第二定律
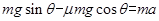 ①
①
由①式解得
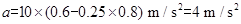 ②
②
(2)设金属棒运动达到稳定时,速度为v、所受安培力为F,棒在沿导轨方向受力平衡
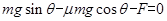 ③
③
此时金属棒克服安培力做功的功率等于电路中电阻R消耗的电功率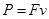 ④
④
由③④两式解得
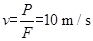 ⑤
⑤
(3)设电路中电流为I,两导轨间金属棒的长为l,磁场的磁感应强度为B
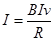 ⑥
⑥
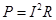 ⑦
⑦
由⑥⑦两式解得
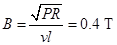
方向垂直于导轨平面向上.
考点:电磁感应定律的应用
点评:解这类问题的突破口为正确分析安培力的变化,根据运动状态列方程求解。

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案 如图所示,处于匀强磁场中的两根足够长、电阻不计的光滑平行金属导轨相距L=1m,导轨平面与水平面成θ=30°角,下端连接阻值为R=0.8Ω的电阻,匀强磁场方向与导轨平面垂直,磁感强度大小B=1T;质量为m=0.1kg、电阻r=0.2Ω金属棒放在两导轨上,棒与导轨垂直并保持良好接触.g取10m/s2.求:
如图所示,处于匀强磁场中的两根足够长、电阻不计的光滑平行金属导轨相距L=1m,导轨平面与水平面成θ=30°角,下端连接阻值为R=0.8Ω的电阻,匀强磁场方向与导轨平面垂直,磁感强度大小B=1T;质量为m=0.1kg、电阻r=0.2Ω金属棒放在两导轨上,棒与导轨垂直并保持良好接触.g取10m/s2.求: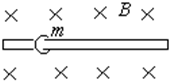 如图所示,质量为m、带电量为+q的滑环,套在水平放置的足够长的固定绝缘横杆上,横杆表面粗糙,整个装置处于磁感强度为B的匀强磁场中,现给滑环一个水平向右的速度v,使其向右运动.(环的直径大于杆的直径,环很小可以当成质点研究)
如图所示,质量为m、带电量为+q的滑环,套在水平放置的足够长的固定绝缘横杆上,横杆表面粗糙,整个装置处于磁感强度为B的匀强磁场中,现给滑环一个水平向右的速度v,使其向右运动.(环的直径大于杆的直径,环很小可以当成质点研究) (2012?上海模拟)如图所示,倾角为α的斜面上放有一通电的矩形线圈,电流方向沿adcba,线圈的ad边和bc边处于水平方向,若整个装置放在一个磁感强度方向竖直向上的匀强磁场之中,线圈处于平衡状态,那么下列说法中正确的有( )
(2012?上海模拟)如图所示,倾角为α的斜面上放有一通电的矩形线圈,电流方向沿adcba,线圈的ad边和bc边处于水平方向,若整个装置放在一个磁感强度方向竖直向上的匀强磁场之中,线圈处于平衡状态,那么下列说法中正确的有( ) 如图所示,一束电子流以速率v通过一个处于矩形空间的大小为B的匀强磁场,速度方向与磁感线垂直.且平行于矩形空间的其中一边,矩形空间边长为
如图所示,一束电子流以速率v通过一个处于矩形空间的大小为B的匀强磁场,速度方向与磁感线垂直.且平行于矩形空间的其中一边,矩形空间边长为