题目内容
如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体.活塞的质量为m,横截面积为S,此时活塞处于平衡状态,气体的温度为T1.现通过电热丝缓慢加热气体,在气体吸收热量为Q的过程中,气体对活塞做功的大小为W.已知大气压强为p,重力加g,不计活塞与气缸的摩擦.求:(1)气体的压强;
(2)加热过程中气体的内能增加量;
(3)现停止对气体加热,同时在活塞上缓慢添加砂粒,当添加砂粒的质量为m时,活塞恰好回到原来的位置,求此时气体的温度.
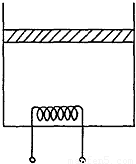
【答案】分析:(1)由题,活塞处于平衡状态,根据平衡条件列式求气体的压强;
(2)根据热力学第一定律求得气体的内能增加量;
(3)当添加砂粒的质量为m时,活塞恰好回到原来的位置,再以活塞为研究对象,由平衡条件求得封闭气体的压强,由查理定律列式求此时气体的温度.
解答:解:(1)活塞处于平衡状态,由力的平衡可知,p1S=pS+mg,解得气体的压强p1=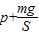
(2)由热力学第一定律可知,加热过程中气体的内能增加量
△U=Q-W
(3)末状态时,再对活塞研究,得到气体的压强 p2=p+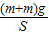
由于气体的初始状态和末状态体积相同,由查理定律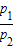 =
=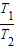
可得:T2=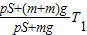
答:
(1)气体的压强是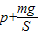 ;
;
(2)加热过程中气体的内能增加量是Q-W;
(3)此时气体的温度是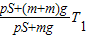 .
.
点评:(1)确做功与热量的正负的确定是解题的关键;(2)对气体正确地进行受力分析,求得两个状态的压强是解题的关键.属于中档题.
(2)根据热力学第一定律求得气体的内能增加量;
(3)当添加砂粒的质量为m时,活塞恰好回到原来的位置,再以活塞为研究对象,由平衡条件求得封闭气体的压强,由查理定律列式求此时气体的温度.
解答:解:(1)活塞处于平衡状态,由力的平衡可知,p1S=pS+mg,解得气体的压强p1=
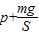
(2)由热力学第一定律可知,加热过程中气体的内能增加量
△U=Q-W
(3)末状态时,再对活塞研究,得到气体的压强 p2=p+
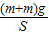
由于气体的初始状态和末状态体积相同,由查理定律
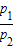 =
=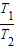
可得:T2=
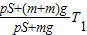
答:
(1)气体的压强是
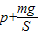 ;
;(2)加热过程中气体的内能增加量是Q-W;
(3)此时气体的温度是
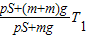 .
.点评:(1)确做功与热量的正负的确定是解题的关键;(2)对气体正确地进行受力分析,求得两个状态的压强是解题的关键.属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(1)如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体.活塞的质量为m,横截面积为S,与容器底部相距H.现通过电热丝缓慢加热气体,活塞逐渐上升,活塞与缸壁间摩擦不计.下列说法正确的是_______________
| A.上述过程气体做等压膨胀,温度升高 |
| B.上述过程气体做绝热膨胀,温度升高 |
| C.气体的吸收热量大于它对外做功,内能增加 |
| D.气体吸收的热量等于它对外做功,内能不变 |
 如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体,活塞的质量为m,横截面积为S,与容器底部相距h.现通过电热丝缓慢加热气体,当气体吸收热量Q时,活塞上升高度h,此时气体的温度为T1.已知大气压强为p0,重力加速度为g,不计活塞与气缸的摩擦.求:
如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体,活塞的质量为m,横截面积为S,与容器底部相距h.现通过电热丝缓慢加热气体,当气体吸收热量Q时,活塞上升高度h,此时气体的温度为T1.已知大气压强为p0,重力加速度为g,不计活塞与气缸的摩擦.求: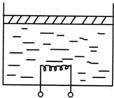 如图所示,一圆柱形绝热容器竖直放置,通过绝热活塞封闭着摄氏温度为t1的理想气体,活塞的质量为m,横截面积为S,与容器底部相距h1.现通过电热丝给气体加热一段时间,使其温度上升到t2,若这段时间内气体吸收的热量为Q,已知大气压强为P0,重力加速度为g,求:
如图所示,一圆柱形绝热容器竖直放置,通过绝热活塞封闭着摄氏温度为t1的理想气体,活塞的质量为m,横截面积为S,与容器底部相距h1.现通过电热丝给气体加热一段时间,使其温度上升到t2,若这段时间内气体吸收的热量为Q,已知大气压强为P0,重力加速度为g,求: