题目内容
如图所示，半径分别为R，r(R＞r)的甲、乙两圆形轨道安置在同一竖直平面内，两轨道之间由一条水平轨道CD相连，如小球从斜面较高处滑下，可以滑过甲轨道，经过CD段滑到乙轨道．小球与CD段间的动摩擦因数为μ，其余各段均光滑，现有一小球从高为3R的斜面上A点由静止释放，为避免出现小球脱离圆形轨道的现象，试设计CD段可取的长度．
答案：
解析：
解析：
|
要求小球不脱离圆形轨道，可分以下两种情形讨论 (1)小球能通过乙轨道的最高点：则有
mg＋FN＝m· 对小球运动的全过程由能量守恒有：
mg·3R＝ 又知FN≥0．由上式解得
此后小球一直在乙轨道做圆周运动． (2)小球达乙轨道某点时速度为0，某高度为h，满足h＜r由能量守恒有
mg3R＝mgh＋μmg 解得：
此后小球在乙轨道内做往复运动． |
，①
mv2＋mg·2r＋μmg
，②
＜
，
，
练习册系列答案
相关题目
如图所示，半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上，轨道之间有一条水平轨道CD相通，一个小球以一定的速度先滑上甲轨道，通过动摩擦因数为μ的CD段，又滑上乙轨道，最后离开两圆轨道，若小球在两圆轨道的最高点对轨道的压力都恰好为零．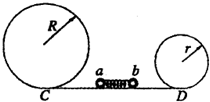 
如图所示，半径分别为R和r（R＞r）的甲乙两光滑圆轨道安置在同一竖直平面内，两轨道之间由一条光滑水平轨道CD相连，在水平轨道CD上一轻弹簧a、b被两小球夹住，同时释放两小球，a、b球恰好能通过各自的圆轨道的最高点，求：
（2011?信阳二模）如图所示，半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上，轨道之间有一条水平轨道CD相通，一小球以一定的速度先滑上甲轨道，又滑上乙轨道，最后离开两圆轨道．通过动摩擦因数为μ的CD段，若小球在两圆轨道的最高点对轨道压力都恰好为零，且CD段的动摩擦因数为μ，试求水平CD段的长度．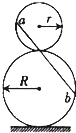
如图所示，半径分别为r和R的圆环竖直叠放（相切）于水平面上，一条公共斜弦过两圆切点且分别与两圆相交于a、b两点．在此弦上铺一条光滑轨道，且令一小球从b点以某一初速度沿轨道向上抛出，设小球穿过切点时不受阻挡．若该小球恰好能上升到a点，则该小球从b点运动到a点所用时间为多少？
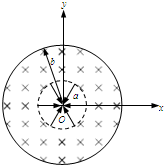如图所示，半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场，中心O处固定一个半径很小（可忽略）的金属球，在小圆空间内存在沿半径向内的辐向电场，小圆周与金属球间电势差为U，两圆之间的空间存在垂直于纸面向里的匀强磁场，设有一个带负电的粒子从金属球表面沿+x轴方向以很小的初速度逸出，粒子质量为m，电量为q，（不计粒子重力，忽略粒子初速度）求：