题目内容
6.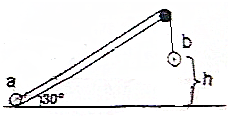 如图,一根不可伸长的轻绳跨过光滑定滑轮,绳两端各系一个小球a和b,a球质量为m,静止于倾斜角为30°的光滑固定斜面的底端,b球质量为3m,用手托住,离地面高度为h,此时轻绳刚好拉紧,从静止开始释放b后,a可能达到的最大高度为(设a球沿斜面向上运动未离开斜面)( )
如图,一根不可伸长的轻绳跨过光滑定滑轮,绳两端各系一个小球a和b,a球质量为m,静止于倾斜角为30°的光滑固定斜面的底端,b球质量为3m,用手托住,离地面高度为h,此时轻绳刚好拉紧,从静止开始释放b后,a可能达到的最大高度为(设a球沿斜面向上运动未离开斜面)( )| A. | h | B. | 1.125h | C. | 2h | D. | 2.5h |
分析 释放物块b到落地的过程中,a、b组成的系统只有重力做功,机械能守恒,根据机械能守恒定律列式,可求出物体b着地时a的速度.
b落地后,a继续沿斜面上升,再根据动能定理求出m上升的距离,即可得到a能沿到达的最大高度.
解答 解:设b落地时的速度为v,系统的机械能守恒得:
3mgh-mgsin30°h=$\frac{1}{2}$(3m+m)v2
解得:v=$\frac{\sqrt{5gh}}{2}$
物块b落地后,a以v为初速度沿斜面匀减速上升,设沿斜面又上升的高度为h′.
对a,由动能定理得:-mgh′=0-$\frac{1}{2}$mv2,
则得:h′=$\frac{{v}^{2}}{2g}$=0.625h
故a可能达到的最大高度为:
H=hsin30°+h′=1.125h
故选:B.
点评 本题中单个物体机械能不守恒,但二者组成的系统机械能守恒.求a能沿斜面滑行的最大高度是相对斜面底边的.

练习册系列答案
相关题目
17.下列物理量均属于矢量的一组是( )
| A. | 质量,重力 | B. | 动能,电流 | C. | 速度,速率 | D. | 位移,速度 |
14.鸡蛋碰石头,鸡蛋碎,石头完好无损,以下判断正确的是( )
| A. | 鸡蛋碎了,说明鸡蛋受到的撞击力大 | |
| B. | 石头完好无损,说明石头受到的撞击力小 | |
| C. | 鸡蛋和石头受到的撞击力一样大 | |
| D. | 必须用仪器检测才知道谁受到的撞击力大 |
11.如图所示的四个图象中,描述物体做匀加速直线运动的是( )
| A. |  | B. |  | C. |  | D. |  |
18.一台理想变压器,原线圈与副线圈的匝数分别为1100和180,现将变压器原线圈接在交流电源上,设输入电压为U1,输出电压为U2,那么( )
| A. | 若U1=220V,则U2=36V | B. | 若U1=220V,则U2=16V | ||
| C. | 若U1=110V,则U2=36V | D. | 若U1=110V,则U2=18V |
16.某同学甲将一小球从手中以初速度v1竖直向上抛出,由于空气阻力,测得小球回到甲手中时速度大小为v2(v2<v1),已知重力加速度为g,下面是同学乙和同学丙分别建立的两种不同的物理模型.
①同学乙假定空气阻力大小恒定
②同学丙假定空气阻力大小与速度大小成正比
(1)根据乙同学建立的物理模型计算出小球上升的最大高度H;
(2)根据丙同学建立的物理模型计算出小球运动的时间t;
则下列表达式正确的是( )
①同学乙假定空气阻力大小恒定
②同学丙假定空气阻力大小与速度大小成正比
(1)根据乙同学建立的物理模型计算出小球上升的最大高度H;
(2)根据丙同学建立的物理模型计算出小球运动的时间t;
则下列表达式正确的是( )
| A. | H=$\frac{{{v}_{1}}^{2}+{{v}_{2}}^{2}}{2g}$ | B. | H=$\frac{{{v}_{1}}^{2}+{{v}_{2}}^{2}}{4g}$ | C. | t=$\frac{{v}_{1}+{v}_{2}}{2g}$ | D. | t=$\frac{{v}_{1}+{v}_{2}}{g}$ |
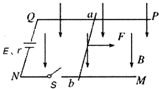 如图所示,一对足够长的平行光滑金属导轨固定在水平面上,两导轨间距为L,左端接一电源,其电动势为E,内电阻为r,有一质量为m、长度也为L的金属棒静置于导轨上,且与导轨垂直,金属棒的电阻为R,导轨电阻可忽略不计,整个装置处于磁感应强度为B,方向竖直向下的匀强磁场中,
如图所示,一对足够长的平行光滑金属导轨固定在水平面上,两导轨间距为L,左端接一电源,其电动势为E,内电阻为r,有一质量为m、长度也为L的金属棒静置于导轨上,且与导轨垂直,金属棒的电阻为R,导轨电阻可忽略不计,整个装置处于磁感应强度为B,方向竖直向下的匀强磁场中,