题目内容
 如图所示,光滑绝缘的水平地面上相距2L的A、B两点固定有两个电量均为Q的正电荷,a、O、b是AB连线上的三点,且O为中点,
如图所示,光滑绝缘的水平地面上相距2L的A、B两点固定有两个电量均为Q的正电荷,a、O、b是AB连线上的三点,且O为中点,. |
| oa |
. |
| ob |
| L |
| 2 |
|
(1)a点的场强
(2)a点的电势;
(3)电荷q在电场中运动的总路程.
分析:(1)根据场强的叠加,通过点电荷的场强公式求出a点的场强.
(2)对a到o、a到b运用动能定理,抓住a到b过程中电场力做功为零,求出a到o过程中电场力做功,从而得出ao的电势差,根据o点电势为零,求出a点的电势.
(3)对a到b过程运用动能定理求出阻力的大小,然后对全过程研究,运用能量守恒定律求出通过的路程.
(2)对a到o、a到b运用动能定理,抓住a到b过程中电场力做功为零,求出a到o过程中电场力做功,从而得出ao的电势差,根据o点电势为零,求出a点的电势.
(3)对a到b过程运用动能定理求出阻力的大小,然后对全过程研究,运用能量守恒定律求出通过的路程.
解答:解:(1)a点的场强为A、B两点点电荷产生场强的合场强,即:
Ea=k
-k
=
,方向有A指向B.
(2)因为O点电势为0,所以a点电势一定为正值,因为到b时速度是零,所以点电荷必带正电.
从a到o,根据动能定理得:W电+W阻=(n-1)?
mv02.
从a到b,根据动能定理得:2W阻=0-
mv02.
解得:W电=
则:Uao=
=
所以a点的电势为:
.
(3)如果不停在o点,那电荷在电场力作用下还会运动,所以电荷停在o.
对全程,由能量守恒定律得:
mv02+qUao=fs
由a到b,根据动能定理得:-fL=0-
mv02
可得阻力:f=
解得:s=
L.
答:(1)a点的场强为
,方向有A指向B.
(2)a点的电势为
.
(3)电荷q在电场中运动的总路程为
L.
Ea=k
| Q | ||
(
|
| Q | ||
(
|
| 32kQ |
| 9L2 |
(2)因为O点电势为0,所以a点电势一定为正值,因为到b时速度是零,所以点电荷必带正电.
从a到o,根据动能定理得:W电+W阻=(n-1)?
| 1 |
| 2 |
从a到b,根据动能定理得:2W阻=0-
| 1 |
| 2 |
解得:W电=
| (2n-1)mv02 |
| 4 |
则:Uao=
| W电 |
| q |
| (2n-1)mv02 |
| 4q |
所以a点的电势为:
| (2n-1)mv02 |
| 4q |
(3)如果不停在o点,那电荷在电场力作用下还会运动,所以电荷停在o.
对全程,由能量守恒定律得:
| 1 |
| 2 |
由a到b,根据动能定理得:-fL=0-
| 1 |
| 2 |
可得阻力:f=
| mv02 |
| 2L |
解得:s=
| 2n+1 |
| 2 |
答:(1)a点的场强为
| 32kQ |
| 9L2 |
(2)a点的电势为
| (2n-1)mv02 |
| 4q |
(3)电荷q在电场中运动的总路程为
| 2n+1 |
| 2 |
点评:本题综合考查了场强的叠加、电场力做功与电势差的关系、动能定理、能量守恒定律等,综合性较强,对学生能力要求较高,需加强训练.

练习册系列答案
相关题目
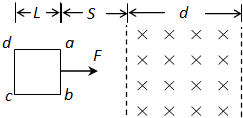 如图所示,光滑绝缘的水平面内有竖直方向的宽度为d的匀强磁场区,磁场的磁感应强度为B.正方形金属线框abcd边长为L(L<d),质量为m,现对线框施加垂直于ab边的水平恒力F使线框从磁场左侧距磁场S处由静止开始运动,如果ab边刚进入磁场时的速度为v0,cd边刚穿出磁场时的速度也为v0,则从ab边刚进入磁场到cd边刚穿出磁场的整个过程( )
如图所示,光滑绝缘的水平面内有竖直方向的宽度为d的匀强磁场区,磁场的磁感应强度为B.正方形金属线框abcd边长为L(L<d),质量为m,现对线框施加垂直于ab边的水平恒力F使线框从磁场左侧距磁场S处由静止开始运动,如果ab边刚进入磁场时的速度为v0,cd边刚穿出磁场时的速度也为v0,则从ab边刚进入磁场到cd边刚穿出磁场的整个过程( )| A、线框有一阶段在做匀加速运动 | B、线框ab边在刚进入磁场时可能做加速运动 | C、线框ab边在刚穿出磁场时一定是先做减速运动 | D、线框中产生的热量为F(d+S+L) |
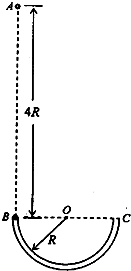 如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直平面内,管口B、C的连线是水平直径.现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R.从小球进入管口开始,整个空间突然加上一个匀强电场,电场力在竖直向上的分力大小与重力大小相等,结果小球从管口C处脱离圆管后,其运动轨迹最后经过A点.设小球运动过程中带电量没有改变,重力加速度为g.求:
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直平面内,管口B、C的连线是水平直径.现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R.从小球进入管口开始,整个空间突然加上一个匀强电场,电场力在竖直向上的分力大小与重力大小相等,结果小球从管口C处脱离圆管后,其运动轨迹最后经过A点.设小球运动过程中带电量没有改变,重力加速度为g.求: 如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直面内,管口B,C的连线水平.质量为m的带正电小球从B点正上方的A点自由下落A,B两点间距离为4R.从小球(小球直径小于细圆管直径)进人管口开始,整个空间中突然加上一个斜向左上方的匀强电场,小球所受电场力在竖直方向上的分力方向向上,大小与重力相等,结果小球从管口 C处离开圆管后,又能经过A点.设小球运动过程中电荷量没有改变,重力加速度为g,求:
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直面内,管口B,C的连线水平.质量为m的带正电小球从B点正上方的A点自由下落A,B两点间距离为4R.从小球(小球直径小于细圆管直径)进人管口开始,整个空间中突然加上一个斜向左上方的匀强电场,小球所受电场力在竖直方向上的分力方向向上,大小与重力相等,结果小球从管口 C处离开圆管后,又能经过A点.设小球运动过程中电荷量没有改变,重力加速度为g,求: 如图所示,光滑绝缘的水平面上方,左边有垂直纸面向里的匀强磁场,右边有竖直向上的匀强电场.质量为m,带电量为q(正电)的点电荷 a,以水平向右的初速度v沿水平面进入匀强磁场和匀强电场,恰好都不脱离水平面.在匀强电场中用绝缘细线悬挂一个质量为m的不带电的小球b(可视为质点),小球处于静止且对水平面无压力.点电荷a进入匀强电场后与小球b正碰并粘在一起,恰好能绕悬挂点O在匀强电场中做竖直面内的圆周运动.(重力加速度为g)求:
如图所示,光滑绝缘的水平面上方,左边有垂直纸面向里的匀强磁场,右边有竖直向上的匀强电场.质量为m,带电量为q(正电)的点电荷 a,以水平向右的初速度v沿水平面进入匀强磁场和匀强电场,恰好都不脱离水平面.在匀强电场中用绝缘细线悬挂一个质量为m的不带电的小球b(可视为质点),小球处于静止且对水平面无压力.点电荷a进入匀强电场后与小球b正碰并粘在一起,恰好能绕悬挂点O在匀强电场中做竖直面内的圆周运动.(重力加速度为g)求: 如图所示,光滑绝缘的斜面倾角为37°,一带电量为+q的小物体质量为m,置于斜面上,当沿水平方向加一如图所示的匀强电场时,小物体恰好处于静止状态,从某时刻开始,电场强度突然减为原来的
如图所示,光滑绝缘的斜面倾角为37°,一带电量为+q的小物体质量为m,置于斜面上,当沿水平方向加一如图所示的匀强电场时,小物体恰好处于静止状态,从某时刻开始,电场强度突然减为原来的