题目内容
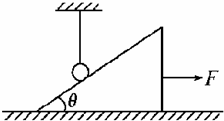如图所示，斜面体质量为M，倾角为θ，与水平面间的动摩擦因数为μ，用细绳竖直悬挂一质量为m小球静止在光滑斜面上，当烧断绳的瞬间，至少以多大的水平向右的力由静止拉动斜面体，小球才能做自由落体运动到地面？分析：根据小球自由下落的位移公式列式；再根据牛顿第二定律和位移时间公式列式；根据几何关系找出小球位移和斜面体位移的关系；最后联立方程组求解．
解答：解：设小球自由落体运动到地面上，下落高度为h，
则斜面体至少水平向右运动的位移为：x=h?cotθ
对小球：h=
gt2
对斜面体：x=
at2
由以上三式解得：a=gcotθ
以斜面体为研究对象有：F-μMg=Ma
所以F=μMg+Mgcotθ=（μ+cotθ）Mg．
即当烧断绳的瞬间，至少以（μ+cotθ）Mg的水平向右的力由静止拉动斜面体，小球才能做自由落体运动到地面．
则斜面体至少水平向右运动的位移为：x=h?cotθ
对小球：h=
| 1 |
| 2 |
对斜面体：x=
| 1 |
| 2 |
由以上三式解得：a=gcotθ
以斜面体为研究对象有：F-μMg=Ma
所以F=μMg+Mgcotθ=（μ+cotθ）Mg．
即当烧断绳的瞬间，至少以（μ+cotθ）Mg的水平向右的力由静止拉动斜面体，小球才能做自由落体运动到地面．
点评：本题关键是找出木板位移和小球位移的几何关系，然后根据牛顿第二定律和位移时间关系公式联立求解．
练习册系列答案
相关题目
如图所示，斜面体质量为M，倾角为θ，置于水平地面上，当质量为m的小木块沿斜面匀速下滑时，斜面体仍静止不动．则（ ）
如图所示，斜面体质量为M，放在粗糙的水平面上．一滑块质量为m，放在斜面体上，由静止开始加速下滑，在滑块下滑过程中斜面体始终保持静止． 则在滑块下滑过程中（ ）
如图所示，斜面体质量为M，倾角为θ，置于水平地面上，当质量为m的小木块沿斜面体的光滑斜面自由下滑时，斜面体仍静止不动．则（ ）| A、斜面体受地面的支持力等于（m+M）g | B、斜面体受地面的支持力小于（m+M）g | C、斜面体受地面的摩擦力为零 | D、斜面体受地面的摩擦力不为零 |