题目内容
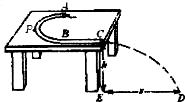 如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0m,BC段长L=1.5m.弹射装置将一个质量m=0.1Kg的小球(可视为质点)以v0=5m/s的水平初速度从A点弹入轨道,小球从C点离开轨道随即水平抛出,落地点D离开C的水平距离s=2m,不计空气阻力,g取10m/s2,求:
如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0m,BC段长L=1.5m.弹射装置将一个质量m=0.1Kg的小球(可视为质点)以v0=5m/s的水平初速度从A点弹入轨道,小球从C点离开轨道随即水平抛出,落地点D离开C的水平距离s=2m,不计空气阻力,g取10m/s2,求:(1)小球在半圆轨道上运动时的角速度ω和加速度a的大小
(2)小球在半圆轨道上运动时向心力的大小
(3)小球从A点运动到C点的时间t
(4)桌子的高度h.
分析:(1)小球在半圆形APB管内做匀速圆周运动,角速度为ω=
,加速度a=ωv0.
(2)根据牛顿第二定律求出向心力的大小;
(3)小球离开圆管后先做匀速直线运动,离开桌面后做平抛运动,根据运动学公式分别求出A到B和B到C的运动时间,从而求出小球从A到C的时间.
(4)根据平抛运动水平方向上运动的时间和竖直方向上运动的时间相等,求出桌子的高度.
| v0 |
| R |
(2)根据牛顿第二定律求出向心力的大小;
(3)小球离开圆管后先做匀速直线运动,离开桌面后做平抛运动,根据运动学公式分别求出A到B和B到C的运动时间,从而求出小球从A到C的时间.
(4)根据平抛运动水平方向上运动的时间和竖直方向上运动的时间相等,求出桌子的高度.
解答:解:(1)小球在半圆形APB管内做匀速圆周运动时,角速度为ω=
=
rad/s=5rad/s.
加速度为:a=ωv0=5×5m/s2=25m/s2.
(2)设向心力的大小为F,根据牛顿第二定律得,F=ma=0.1×25N=2.5N.
(3)小球从A到B的时间 t1=
=
s,从B到C做匀速直线运动,时间为t2=
=
s=0.3s
故小球从A点运动到C点的时间:t=t1+t2=
s+0.3s≈0.93s;
(4)小球从C到D的过程做平抛运动,则有:
h=
gt2
s=v0t;
联立得:h=
=
m=0.8m;
答:
(1)小球在半圆轨道上运动时的角速度ω为5rad/s,加速度a的大小为25m/s2.
(2)小球在半圆轨道上运动时向心力的大小为2.5N.
(3)小球从A点运动到C点的时间t约为0.93s;
(4)桌子的高度h为0.8m.
| v0 |
| R |
| 5 |
| 1 |
加速度为:a=ωv0=5×5m/s2=25m/s2.
(2)设向心力的大小为F,根据牛顿第二定律得,F=ma=0.1×25N=2.5N.
(3)小球从A到B的时间 t1=
| πR |
| v0 |
| π |
| 5 |
| L |
| v0 |
| 1.5 |
| 5 |
故小球从A点运动到C点的时间:t=t1+t2=
| π |
| 5 |
(4)小球从C到D的过程做平抛运动,则有:
h=
| 1 |
| 2 |
s=v0t;
联立得:h=
| s2g | ||
2
|
| 22×10 |
| 2×52 |
答:
(1)小球在半圆轨道上运动时的角速度ω为5rad/s,加速度a的大小为25m/s2.
(2)小球在半圆轨道上运动时向心力的大小为2.5N.
(3)小球从A点运动到C点的时间t约为0.93s;
(4)桌子的高度h为0.8m.
点评:解决本题的关键知道角速度、加速度与线速度的关系,以及知道平抛运动在水平方向和竖直方向上的运动规律,知道分运动与合运动具有等时性.

练习册系列答案
相关题目
 (2012?浦东新区一模)如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0m,BC段长L=1.5m.弹射装置将一个小球(可视为质点)以v0=5m/s的水平初速度从A点弹入轨道,小球从C点离开轨道随即水平抛出,落地点D离开C的水平距离s=2m,不计空气阻力,g取10m/s2.求:
(2012?浦东新区一模)如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0m,BC段长L=1.5m.弹射装置将一个小球(可视为质点)以v0=5m/s的水平初速度从A点弹入轨道,小球从C点离开轨道随即水平抛出,落地点D离开C的水平距离s=2m,不计空气阻力,g取10m/s2.求:
 如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0m,BC段长L=1.5m.弹射装置将一个小球(可视为质点)以v0=5m/s的水平初速度从A点沿切线方向弹入轨道,小球从C点离开轨道随即水平抛出,落地点D离开C的水平距离s=2m,不计空气阻力,g取10m/s2.求:
如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0m,BC段长L=1.5m.弹射装置将一个小球(可视为质点)以v0=5m/s的水平初速度从A点沿切线方向弹入轨道,小球从C点离开轨道随即水平抛出,落地点D离开C的水平距离s=2m,不计空气阻力,g取10m/s2.求: 如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0m,BC段长L=1.5m.弹射装置将一个质量为1kg的小球(可视为质点)以v0=5m/s的水平初速度从A点弹入轨道,小球从C点离开轨道随即水平抛出,桌子的高度h=1.2m,不计空气阻力,g取10m/s2.求:
如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0m,BC段长L=1.5m.弹射装置将一个质量为1kg的小球(可视为质点)以v0=5m/s的水平初速度从A点弹入轨道,小球从C点离开轨道随即水平抛出,桌子的高度h=1.2m,不计空气阻力,g取10m/s2.求: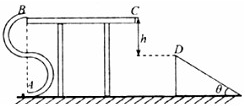 如图所示,用内壁光滑的薄壁细管弯成的“S”形轨道固定于竖直平面内,其弯曲部分是由两个半径均为R=0.2m 的半圆平滑对接而成(圆的半径远大于细管内径).轨道底端A与水平地面相切,顶端与一个长为l=0.9m的水平轨道相切B点.一倾角为θ=37°的倾斜轨道固定于右侧地面上,其顶点D与水平轨道的高度差为h=0.45m,并与其它两个轨道处于同一竖直平面内.一质量为m=0.1kg 的小物体(可视为质点)在A点被弹射入“S”形轨道内,沿轨道ABC运动,并恰好从D点无碰撞地落到倾斜轨道上.小物体与BC段间的动摩擦因数μ=0.5. (不计空气阻力,g取10m/s2.sin37°=0.6,cos37°=0.8)
如图所示,用内壁光滑的薄壁细管弯成的“S”形轨道固定于竖直平面内,其弯曲部分是由两个半径均为R=0.2m 的半圆平滑对接而成(圆的半径远大于细管内径).轨道底端A与水平地面相切,顶端与一个长为l=0.9m的水平轨道相切B点.一倾角为θ=37°的倾斜轨道固定于右侧地面上,其顶点D与水平轨道的高度差为h=0.45m,并与其它两个轨道处于同一竖直平面内.一质量为m=0.1kg 的小物体(可视为质点)在A点被弹射入“S”形轨道内,沿轨道ABC运动,并恰好从D点无碰撞地落到倾斜轨道上.小物体与BC段间的动摩擦因数μ=0.5. (不计空气阻力,g取10m/s2.sin37°=0.6,cos37°=0.8)